已知数列{an}满足条件: a1=1,a2=r(r＞0),且{anan+1}是公比为q(q＞0)的等比数列，设bn=a2n－1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2＞an+2an+3(n∈N*)成立的q的取值范围；
(2)求bn和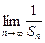
，其中Sn=b1+b2+…+bn；
(3)设r=219.2－1，q=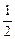
，求数列{
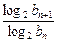}的最大项和最小项的值.
推荐套卷
已知数列{an}满足条件: a1=1,a2=r(r＞0),且{anan+1}是公比为q(q＞0)的等比数列，设bn=a2n－1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2＞an+2an+3(n∈N*)成立的q的取值范围；
(2)求bn和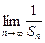，其中Sn=b1+b2+…+bn；
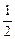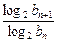(3)设r=219.2－1，q=，求数列{}的最大项和最小项的值.
粤公网安备 44130202000953号