{an}为等差数列，公差d≠0,an≠0,(n∈N*),且akx2+2ak+1x+ak+2=0(k∈N*)
(1)求证:当k取不同自然数时，此方程有公共根；
(2)若方程不同的根依次为x1,x2,…,xn,…,
求证:数列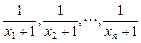
为等差数列.
相关试题
,
,且
．
且
，求
的值；
＝
，求
是定义在
上的单调奇函数, 且
.
.
是定义在
上的偶函数，当
时，
．
时
的单调区间，并证明你的结论；
且
，证明：
.
，
,它们定义域的交集为
,若对任意的
,
，则称
是集合
的元素.
是否是
，求
，并判断
与直线
相切于点
．
的解析式；
，不等式
恒成立，求实数
的取值范围．相关知识点
推荐套卷
{an}为等差数列，公差d≠0,an≠0,(n∈N*),且akx2+2ak+1x+ak+2=0(k∈N*)
(1)求证:当k取不同自然数时，此方程有公共根；
(2)若方程不同的根依次为x1,x2,…,xn,…,
求证:数列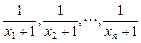为等差数列.
粤公网安备 44130202000953号