在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…,对每个自然数n点Pn位于函数y=2000( )x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
)x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
(1)求点Pn的纵坐标bn的表达式;
(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由.
推荐套卷
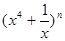 的展开式中,第三项的二项式系数比第二项的二项式系数大35。
的展开式中,第三项的二项式系数比第二项的二项式系数大35。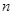 的值;(2)求展开式中的常数项。
的值;(2)求展开式中的常数项。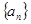 的前
的前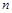 项和
项和 是二项式
是二项式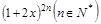 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.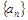 的通项公式;
的通项公式; ,求
,求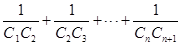 的值.
的值. 中,动点
中,动点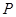 到两点
到两点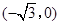 ,
,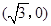 的距离之和等于
的距离之和等于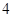 ,设点
,设点 ,直线
,直线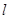 过点
过点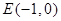 且与曲线
且与曲线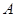 ,
,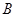 两点.
两点.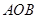 面积的最大值,若存在,求出△
面积的最大值,若存在,求出△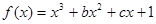 在区间
在区间 ,
,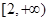 上单调递增,在区间[-2,2]上单调递减.
上单调递增,在区间[-2,2]上单调递减.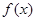 的解析式;
的解析式;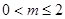 ,若对任意的x1、x2
,若对任意的x1、x2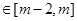 不等式
不等式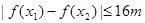 恒成立,求实数m的最小值。
恒成立,求实数m的最小值。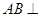 平面
平面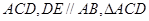 是正三角形,且
是正三角形,且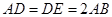 .
.
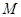 是线段
是线段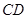 的中点,求证:
的中点,求证: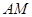 ∥平面
∥平面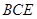 ;
;  与平面
与平面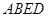 所成角的余弦值.
所成角的余弦值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号