一台仪器每启动一次都随机地出现一个5位二进制数
| A1 |
A2 |
A3 |
A4 |
A5 |
A=
其中A1=1,Ak(k=2,3,4,5)为0的概率为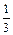 ,为1的概率为
,为1的概率为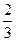 .例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
.例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
(1)P(m="3) " (2)P(m≤3)
相关知识点
推荐套卷
一台仪器每启动一次都随机地出现一个5位二进制数
| A1 |
A2 |
A3 |
A4 |
A5 |
A=
其中A1=1,Ak(k=2,3,4,5)为0的概率为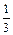 ,为1的概率为
,为1的概率为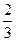 .例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
.例如若A=10001,其中A1= A5=1,A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时,
(1)P(m="3) " (2)P(m≤3)