由原点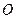 向三次曲线
向三次曲线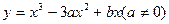 引切线,切于不同于点
引切线,切于不同于点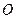 的点
的点 ,再由
,再由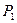 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于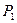 的点
的点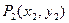 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列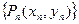 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求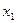 ; (2)求
; (2)求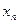 与
与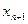 的关系式;
的关系式;
(3)若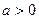 ,求证:当
,求证:当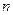 为正偶数时,
为正偶数时,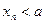 ;当
;当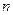 为正奇数时,
为正奇数时,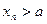 .
.
推荐套卷
由原点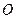 向三次曲线
向三次曲线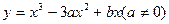 引切线,切于不同于点
引切线,切于不同于点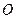 的点
的点 ,再由
,再由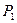 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于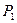 的点
的点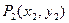 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列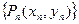 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求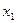 ; (2)求
; (2)求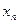 与
与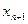 的关系式;
的关系式;
(3)若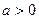 ,求证:当
,求证:当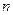 为正偶数时,
为正偶数时,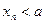 ;当
;当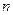 为正奇数时,
为正奇数时,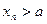 .
.