已知 、
、 、
、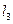 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.
(Ⅰ)如果 与
与 间的距离是1,
间的距离是1, 与
与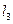 间的距离也是1,可以把一个正三角形
间的距离也是1,可以把一个正三角形 的三顶点分别放在
的三顶点分别放在 ,
, ,
,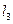 上,求这个正三角形
上,求这个正三角形 的边长;
的边长;
(Ⅱ)如图,如果 与
与 间的距离是1,
间的距离是1, 与
与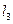 间的距离是2,能否把一个正三角形
间的距离是2,能否把一个正三角形 的三顶点分别放在
的三顶点分别放在 ,
, ,
,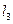 上,如果能放,求
上,如果能放,求 和
和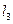 夹角的正切值并求该正三角形边长;如果不能,说明为什么?
夹角的正切值并求该正三角形边长;如果不能,说明为什么?
(Ⅲ)如果边长为2的正三角形 的三顶点分别在
的三顶点分别在 ,
, ,
,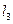 上,设
上,设 与
与 的距离为
的距离为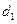 ,
, 与
与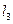 的距离为
的距离为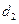 ,求
,求 的范围?
的范围?
推荐套卷
已知 、
、 、
、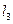 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.
(Ⅰ)如果 与
与 间的距离是1,
间的距离是1, 与
与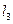 间的距离也是1,可以把一个正三角形
间的距离也是1,可以把一个正三角形 的三顶点分别放在
的三顶点分别放在 ,
, ,
,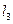 上,求这个正三角形
上,求这个正三角形 的边长;
的边长;
(Ⅱ)如图,如果 与
与 间的距离是1,
间的距离是1, 与
与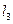 间的距离是2,能否把一个正三角形
间的距离是2,能否把一个正三角形 的三顶点分别放在
的三顶点分别放在 ,
, ,
,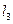 上,如果能放,求
上,如果能放,求 和
和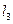 夹角的正切值并求该正三角形边长;如果不能,说明为什么?
夹角的正切值并求该正三角形边长;如果不能,说明为什么?
(Ⅲ)如果边长为2的正三角形 的三顶点分别在
的三顶点分别在 ,
, ,
,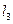 上,设
上,设 与
与 的距离为
的距离为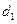 ,
, 与
与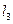 的距离为
的距离为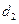 ,求
,求 的范围?
的范围?