已知定义在区间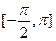
上的函数y＝f（x）的图象关于直线
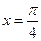对称，当
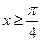时，函数f（x）＝sinx．
（1）求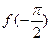
，
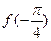的值；
（2）求y＝f（x）的函数表达式；
（3）如果关于x的方程f（x）＝a有解，那么将方程在a取某一确定值时所求得的所有解的和记为Ma，求Ma的所有可能取值及相对应的a的取值范围．
请证明。
推荐套卷
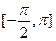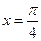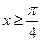已知定义在区间上的函数y＝f（x）的图象关于直线对称，当时，函数f（x）＝sinx．
（1）求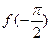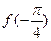，的值；
（2）求y＝f（x）的函数表达式；
（3）如果关于x的方程f（x）＝a有解，那么将方程在a取某一确定值时所求得的所有解的和记为Ma，求Ma的所有可能取值及相对应的a的取值范围．
粤公网安备 44130202000953号