某市统计1994~2004年在校中学生每年高考考入大学的百分比,把农村、县镇、城市分开统计,为了便于计算,把1994年编号为0,1995年编号为1,…,2004年编号为10,如果把每年考入大学的百分比作为统计变量,把年份从0到10作为自变量进行回归分析,可得到下面三条回归直线:
城市: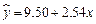 ;
;
县镇: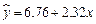 ;
;
农村: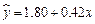 .
.
(1)在同一坐标系中作出三条回归直线;
(2)对于农村学生来讲,系数等于0.42意味着什么?
(3)在这一阶段,哪里的大学入学率增长最快?
推荐套卷
某市统计1994~2004年在校中学生每年高考考入大学的百分比,把农村、县镇、城市分开统计,为了便于计算,把1994年编号为0,1995年编号为1,…,2004年编号为10,如果把每年考入大学的百分比作为统计变量,把年份从0到10作为自变量进行回归分析,可得到下面三条回归直线:
城市: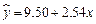 ;
;
县镇: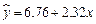 ;
;
农村: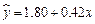 .
.
(1)在同一坐标系中作出三条回归直线;
(2)对于农村学生来讲,系数等于0.42意味着什么?
(3)在这一阶段,哪里的大学入学率增长最快?