如图是某直三棱柱（侧棱与底面垂直）被削去上底后的直观图与三视图的侧视图、俯视图．在直观图中，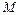
是
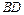的中点.侧视图是直角梯形，俯视图是等腰直角
三角形，有关数据如图所示.
（Ⅰ）求出该几何体的体积；
（Ⅱ）求证：EM∥平面ABC；
(Ⅲ) 试问在棱DC上是否存在点N，使NM⊥平面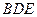
？若存在，确定点N的位置；
若不存在，请说明理由.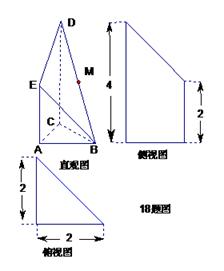
相关试题
内接于⊙
,
,直线
切⊙
,弦
,
相交于点
.
≌△
；
,求
长.
内接于⊙
,
,直线
切⊙
,弦
,
相交于点
.
≌△
；
,求
长.
求证：
；（2）
∽
于
，割线EC交圆O于B，C两点.
，
，求
的大小.
为四边形
的外接圆，且
，
是
延长线上一点，直线
与圆
．推荐套卷
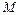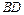如图是某直三棱柱（侧棱与底面垂直）被削去上底后的直观图与三视图的侧视图、俯视图．在直观图中，是的中点.侧视图是直角梯形，俯视图是等腰直角
三角形，有关数据如图所示.
（Ⅰ）求出该几何体的体积；
（Ⅱ）求证：EM∥平面ABC；
(Ⅲ) 试问在棱DC上是否存在点N，使NM⊥平面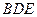？若存在，确定点N的位置；
若不存在，请说明理由.
粤公网安备 44130202000953号