（本小题满分14分）
如图，已知圆
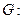
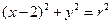是椭圆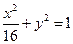
的内接△
的内切圆, 其中
为椭圆的左顶点.
（1）求圆
的半径
;
（2）过点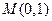
作圆的两条切线交椭圆于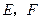
两点，
|
|
证明：直线
与圆相切．
相关试题
已知曲线 y = x3 + x－2 在点 P0 处的切线 
与直线l4x－y－1=0平行，且点 P0 在第三象限,
⑴求P0的坐标; ⑵若直线 
, 且 l 也过切点P0 ,求直线l的方程
（a、b、c、d∈R）图象C关于原点对称，且x=1时，
取极小值
时,求函数f(x)的最大值.
（
的单位为:秒,
的单位为:米/秒）的速度作变速直线运动，求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?
，讨论函数
的单调区间
的首项
，
，
．
是等比数列；
的前
项和
．推荐套卷
（本小题满分14分）
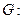
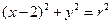如图，已知圆是椭圆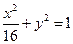的内接△的内切圆, 其中为椭圆的左顶点.
（1）求圆的半径;
（2）过点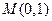作圆的两条切线交椭圆于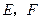两点，
|
|
证明：直线与圆相切．
已知曲线 y = x3 + x－2 在点 P0 处的切线 与直线l4x－y－1=0平行，且点 P0 在第三象限,
⑴求P0的坐标; ⑵若直线 , 且 l 也过切点P0 ,求直线l的方程
粤公网安备 44130202000953号