已知以向量v=(1, 
)为方向向量的直线l过点(0, 
)，抛物线C：
(p>0)的顶点关于直线l的对称点在该抛物线上．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若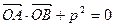
(O为原点，A、B异于原点)，试求点N的轨迹方程．
+x
,且A.B.C三点共线，求
.
数列
且
，
等比数列
且
，
，
分别是
的对称轴
前项和为
，且点
在
图像上，求
的三边长
满足
，
，求
的取值范围．推荐套卷
已知以向量v=(1, )为方向向量的直线l过点(0, )，抛物线C：(p>0)的顶点关于直线l的对称点在该抛物线上．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设A、B是抛物线C上两个动点，过A作平行于x轴的直线m，直线OB与直线m交于点N，若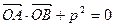(O为原点，A、B异于原点)，试求点N的轨迹方程．
粤公网安备 44130202000953号