已知函数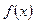 与函数
与函数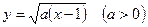 的图像关于直线
的图像关于直线 对称.
对称.
(1)试用含 的代数式表示函数
的代数式表示函数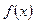 的解析式,并指出它的定义域;
的解析式,并指出它的定义域;
(2)数列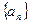 中,
中,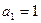 ,当
,当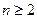 时,
时, .数列
.数列 中,
中,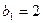 ,
,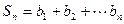 .点
.点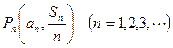 在函数
在函数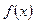 的图像上,求
的图像上,求 的值;
的值;
(3)在(2)的条件下,过点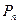 作倾斜角为
作倾斜角为 的直线
的直线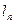 ,则
,则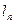 在y轴上的截距为
在y轴上的截距为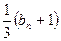
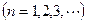 ,求数列
,求数列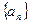 的通项公式.
的通项公式.
推荐套卷
已知函数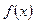 与函数
与函数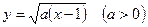 的图像关于直线
的图像关于直线 对称.
对称.
(1)试用含 的代数式表示函数
的代数式表示函数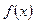 的解析式,并指出它的定义域;
的解析式,并指出它的定义域;
(2)数列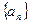 中,
中,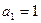 ,当
,当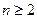 时,
时, .数列
.数列 中,
中,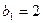 ,
,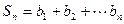 .点
.点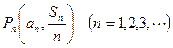 在函数
在函数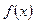 的图像上,求
的图像上,求 的值;
的值;
(3)在(2)的条件下,过点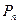 作倾斜角为
作倾斜角为 的直线
的直线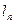 ,则
,则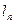 在y轴上的截距为
在y轴上的截距为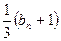
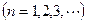 ,求数列
,求数列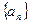 的通项公式.
的通项公式.