甲、乙两地相距s ( km ),汽车从甲地匀速行驶到乙地，速度不得超过c ( km/h ),已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度
的平方成正比，比例系数为2, 固定部分为3000元.
（1）把全程运输成本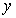
（元）表示为速度的函数。
（2）为了使全程运输成本最小，汽车应以多大的速度行驶？并求最小运输成本。
相关试题
，其中
.
的单调区间；
是曲线
的切线，求实数
的值；
，求
在区间
上的最小值.（
为自然对数的底数）
，求
的集合.
与直角梯形
所在平面互相垂直，
，
，
.
平面
；
的体积.
的单调性，并证明；
，
时，求
；
，求实数
的值.推荐套卷
甲、乙两地相距s ( km ),汽车从甲地匀速行驶到乙地，速度不得超过c ( km/h ),已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度的平方成正比，比例系数为2, 固定部分为3000元.
（1）把全程运输成本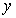（元）表示为速度的函数。
（2）为了使全程运输成本最小，汽车应以多大的速度行驶？并求最小运输成本。
粤公网安备 44130202000953号