以下是某地搜集到的新房屋的销售价格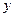
和房屋的面积
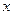的数据： 
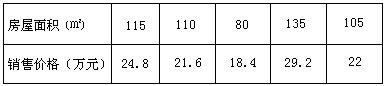
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中加上回归直线；
（3）据（2）的结果估计当房屋面积为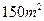
时的销售价格.
，
，求证：
求证：
，
中至少有一个是1．
，
，试求
是纯虚数，求
在复平面内对应点的轨迹．
，求
的最大值和最小值．
；（2）
；
相关知识点
推荐套卷
以下是某地搜集到的新房屋的销售价格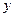和房屋的面积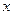的数据：
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中加上回归直线；
（3）据（2）的结果估计当房屋面积为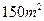时的销售价格.
粤公网安备 44130202000953号