某地政府为科技兴市，欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区（如图中阴影部分），形状为直角梯形QPRE（线段EQ和RP为两个底边），已知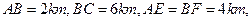
其中AF是以A为顶点、AD为对称轴的抛物线段．试求该高科技工业园区的最大面积．
相关试题
内有一点
，AB为过点
且倾斜角为α的弦，
时，求AB的长;推荐套卷
某地政府为科技兴市，欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区（如图中阴影部分），形状为直角梯形QPRE（线段EQ和RP为两个底边），已知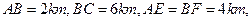其中AF是以A为顶点、AD为对称轴的抛物线段．试求该高科技工业园区的最大面积．
粤公网安备 44130202000953号