已知函数f（x）=ax2+bx+1（a，b为为实数），x∈R．
（1）若函数f（x）的最小值是f（－1）=0，求f（x）的解析式；
（2）在（1）的条件下，f（x）>x+k在区间[－3，－1]上恒成立，试求k的取值范围；
（3）若a>0，f（x）为偶函数，实数m，n满足mn<0，m+n>0，定义函数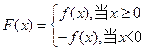
，试判断F（m）+F（n）值的正负，并说明理由．
相关试题
与双曲线
交于A、B，且以AB为直径的圆过原点，求点
的轨迹方程．
(；(2)
．
上两点
，若
，且P点的横坐标为
.
求
；
为数列
的前n项和，若
对一切
都成立，试求a的取值范围.相关知识点
推荐套卷
已知函数f（x）=ax2+bx+1（a，b为为实数），x∈R．
（1）若函数f（x）的最小值是f（－1）=0，求f（x）的解析式；
（2）在（1）的条件下，f（x）>x+k在区间[－3，－1]上恒成立，试求k的取值范围；
（3）若a>0，f（x）为偶函数，实数m，n满足mn<0，m+n>0，定义函数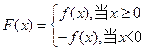，试判断F（m）+F（n）值的正负，并说明理由．
粤公网安备 44130202000953号