已知双曲线的两条渐近线都过坐标原点,且都与以点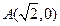 为圆心,
为圆心, 为半径的圆相切,又该双曲线的一个顶点是点
为半径的圆相切,又该双曲线的一个顶点是点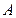 关于直线
关于直线 的对称点。(1)求此双曲线的方程;(2)若直线
的对称点。(1)求此双曲线的方程;(2)若直线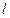 过
过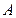 点,且与直线
点,且与直线 垂直,在双曲线上求一点
垂直,在双曲线上求一点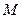 ,使
,使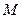 到此直线的距离为
到此直线的距离为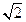 。
。
相关知识点
推荐套卷
已知双曲线的两条渐近线都过坐标原点,且都与以点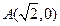 为圆心,
为圆心, 为半径的圆相切,又该双曲线的一个顶点是点
为半径的圆相切,又该双曲线的一个顶点是点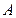 关于直线
关于直线 的对称点。(1)求此双曲线的方程;(2)若直线
的对称点。(1)求此双曲线的方程;(2)若直线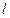 过
过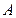 点,且与直线
点,且与直线 垂直,在双曲线上求一点
垂直,在双曲线上求一点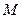 ,使
,使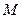 到此直线的距离为
到此直线的距离为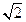 。
。