已知函数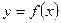 的图像是自原点出发的一条折线,当
的图像是自原点出发的一条折线,当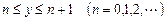 时,该图像是斜率为
时,该图像是斜率为 的线段(其中正常数
的线段(其中正常数 ),设数列
),设数列 由
由 定义.
定义.
Ⅰ.求 、
、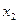 和
和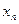 的表达式;
的表达式;
Ⅱ.求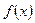 的表达式,并写出其定义域;
的表达式,并写出其定义域;
Ⅲ.证明: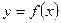 的图像与
的图像与 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.
推荐套卷
已知函数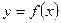 的图像是自原点出发的一条折线,当
的图像是自原点出发的一条折线,当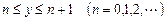 时,该图像是斜率为
时,该图像是斜率为 的线段(其中正常数
的线段(其中正常数 ),设数列
),设数列 由
由 定义.
定义.
Ⅰ.求 、
、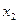 和
和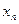 的表达式;
的表达式;
Ⅱ.求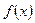 的表达式,并写出其定义域;
的表达式,并写出其定义域;
Ⅲ.证明: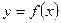 的图像与
的图像与 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.