（本小题满分12分）在△OAB的边OA、OB上分别有一点P、Q,已知
:
＝1:2, 
:
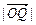＝3:2,连结AQ、BP,设它们交于点R,若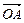
＝a，
＝b. （Ⅰ）用a与 b表示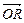
；
（Ⅱ）过R作RH⊥AB,垂足为H,若| a|＝1, | b|＝2, a与 b的夹角
的范围.
中，a1=1，a3=3，求
的值推荐套卷
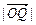（本小题满分12分）在△OAB的边OA、OB上分别有一点P、Q,已知:＝1:2, :＝3:2,连结AQ、BP,设它们交于点R,若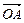＝a，＝b. （Ⅰ）用a与 b表示；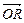
（Ⅱ）过R作RH⊥AB,垂足为H,若| a|＝1, | b|＝2, a与 b的夹角的范围.
粤公网安备 44130202000953号