为了美化环境，构建两型社会，市城建局打算在广场上建造一个绚丽多彩的矩形花园，中间有三个完全一样的矩形花坛，每个花坛面积均为294平方米，花坛四周的过道均为2米，如图所示，设矩形花坛的长为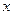
，宽为
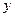，整个矩形花园面积为
。（1）试用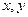
表示S；（2）为了节约用地，当矩形花坛的长为多少米时，新建矩形花园占地最少，占地多少平米？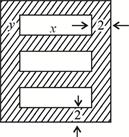
，求该直线倾斜角
的范围．
，
以及一条直线
：
，设长为
的线段
在直线
和
的交点
的轨迹方程．
，
两点的两条直线平行，并且各自绕着
，
旋转，如果两平行线间距离为
．
满足
，求
的最大值和最小值．
：
内有1点
，过
作直角
交圆于
，求动弦
中点的轨迹方程．推荐套卷
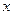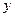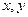为了美化环境，构建两型社会，市城建局打算在广场上建造一个绚丽多彩的矩形花园，中间有三个完全一样的矩形花坛，每个花坛面积均为294平方米，花坛四周的过道均为2米，如图所示，设矩形花坛的长为，宽为，整个矩形花园面积为。（1）试用表示S；（2）为了节约用地，当矩形花坛的长为多少米时，新建矩形花园占地最少，占地多少平米？
粤公网安备 44130202000953号