如果一个数列的各项都是实数，且从第二项开始，每一项与它前一项的平方差是相同的常数，则称该数列为等方差数列，这个常数叫这个数列的公方差．
(1)设数列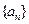
是公方差为
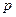（p>0,an >0）的等方差数列，
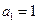求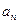
的通项公式；
(2)若数列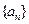既是等方差数列，又是等差数列，证明该数列为常数列
相关试题
（
）．
时，求函数
在
上的最大值和最小值；
的取值范围.
（
）在区间
上有最大值
和最小值
．设
．
、
的值；
在
上有解，求实数
的取值范围.
的图象与
轴相交于点
，且该函数相邻两零点距离为
．
和
的值；
，
，求
值.
：函数
为
上单调减函数,实数
满足不等式
.命题
：当
，函数
。若命题
的取值范围.
，证明：
.相关知识点
推荐套卷
如果一个数列的各项都是实数，且从第二项开始，每一项与它前一项的平方差是相同的常数，则称该数列为等方差数列，这个常数叫这个数列的公方差．
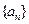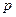(1)设数列是公方差为（p>0,an >0）的等方差数列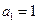，求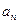的通项公式；
(2)若数列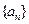既是等方差数列，又是等差数列，证明该数列为常数列
粤公网安备 44130202000953号