有甲、乙、丙、丁四名乒乓球运动员，通过对过去战绩的统计，在一场比赛中，甲对乙、丙、丁取胜的概率分别为0.6，0.8，0.9．
(1)若甲和乙之间进行三场比赛，求甲恰好胜两场的概率；
(2)若四名运动员每两人之间进行一场比赛，设甲获胜场次为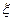
，求随机变量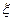的分布列及数学期望
．
.
,
恒成立,求
的最大值;
有且仅有一个实根,求
的取值范围
数列
满足：
是等比数列（要指出首项与公比）, 
的通项公式.
与
互相垂直，其中
．
和
的值；（2）若
，求
的值.
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求
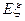推荐套卷
有甲、乙、丙、丁四名乒乓球运动员，通过对过去战绩的统计，在一场比赛中，甲对乙、丙、丁取胜的概率分别为0.6，0.8，0.9．
(1)若甲和乙之间进行三场比赛，求甲恰好胜两场的概率；
(2)若四名运动员每两人之间进行一场比赛，设甲获胜场次为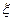，求随机变量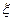的分布列及数学期望．
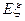粤公网安备 44130202000953号