（本小题满分14分）设函数
（a、b、c、d∈R）图象关于原点对称，且x=1时，
取极小值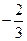
．
（Ⅰ）求函数的解析式；
（Ⅱ）若对任意的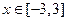
，恒有
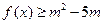成立，求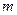
的取值范围；
（Ⅲ）当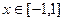
时，函数图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论；
（IV）设表示的曲线为G，过点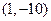
作曲线G的切线
，求的方程．
相关试题
的图象在点
处的切线的倾斜角为
的导函数是
，在（1）条件下，若
的最小值；
的取值范围.
的函数
是奇函数。
的值；
的单调性;
，不等式
恒成立，求
的取值范围．
（a为常数），
的值域.
的定义域为
，且同时满足下列条件：（1）
求
的取值范围
求a的值.推荐套卷
（本小题满分14分）设函数（a、b、c、d∈R）图象关于原点对称，且x=1时，取极小值．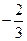
（Ⅰ）求函数的解析式；
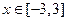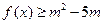（Ⅱ）若对任意的，恒有成立，求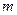的取值范围；
（Ⅲ）当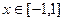时，函数图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论；
（IV）设表示的曲线为G，过点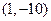作曲线G的切线，求的方程．
粤公网安备 44130202000953号