设
是定义在[-1，1]上的偶函数，
的图象与的图象关于直线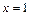
对称，
且当x∈[ 2，3 ] 时，
222233．（1）求的解析式；（2）若在
上为增函数，求
的取值范围；（3）是否存在正整数，使的图象的最高点落在直线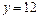
上？若存在，求出的值；若不存在，请说明理由．
求值：
（Ⅰ）
；
.
，求
的值。
，
，求
以及
的值．
, 求
的值.
，母线长为
的圆锥中内接一个高为
的圆柱，求圆柱的表面积推荐套卷
设是定义在[-1，1]上的偶函数，的图象与的图象关于直线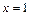对称，
且当x∈[ 2，3 ] 时， 222233．（1）求的解析式；（2）若在上为增函数，求的取值范围；（3）是否存在正整数，使的图象的最高点落在直线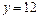上？若存在，求出的值；若不存在，请说明理由．
粤公网安备 44130202000953号