（本小题满分16分）
已知正三角形OAB的三个顶点都在抛物线
上，其中O为坐标原点，设圆C是
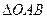的外接圆（点C为圆心）（1）求圆C的方程；（2）设圆M的方程为
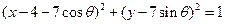，过圆M上任意一点P分别作圆C的两条切线PE、PF，切点为E、F，求
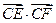的最大值和最小值
相关试题
；②由
推导两角和的正弦公式
•
=3，且 cosB=
，求cosC．
（本小题12分）已知函数
（1）用五点法画出它在一个周期内的闭区间上的图象；
（2）指出
的周期、振幅、初相、对称轴；
（3）说明此函数图象可由
上的图象经怎样的变换得到.
在点
的切线方程为
的值；
时，
的图像与直线
有两个不同的交点，求实数
的取值范围；
，不等式
都成立.
(
)，
的导数为
,且
，若
在
的最小值是2，求实数
的值.
，曲线段
是以点
为顶点且开口向上的抛物线的一段（如图所示）．如果要使矩形的相邻两边分别落在
上，且一个顶点落在曲线段
推荐套卷
（本小题满分16分）
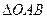已知正三角形OAB的三个顶点都在抛物线上，其中O为坐标原点，设圆C是的外接圆（点C为圆心）（1）求圆C的方程；（2）设圆M的方程为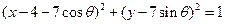，过圆M上任意一点P分别作圆C的两条切线PE、PF，切点为E、F，求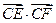的最大值和最小值
（本小题12分）已知函数
（1）用五点法画出它在一个周期内的闭区间上的图象；
（2）指出的周期、振幅、初相、对称轴；
（3）说明此函数图象可由上的图象经怎样的变换得到.
粤公网安备 44130202000953号