（本小题满分14分）
设A(－2，0)，B(2，0)，M为平面上任一点，若|MA|＋|MB|为定值，且cosAMB的最小值为－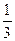
.
(1)求M点轨迹C的方程；(2)过点N(3，0)的直线l与轨迹C及单位圆x2+y2=1自右向左依次交于点P、Q、R、S，若|PQ|＝|RS|，则这样的直线l共有几条？请证明你的结论.
相关试题
的长度是上底面圆周长的
，求由A爬到B的最短路程.
推荐套卷
（本小题满分14分）
设A(－2，0)，B(2，0)，M为平面上任一点，若|MA|＋|MB|为定值，且cosAMB的最小值为－.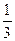
(1)求M点轨迹C的方程；(2)过点N(3，0)的直线l与轨迹C及单位圆x2+y2=1自右向左依次交于点P、Q、R、S，若|PQ|＝|RS|，则这样的直线l共有几条？请证明你的结论.
粤公网安备 44130202000953号