给出定义:若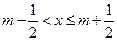 (其中
(其中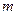 为整数),则
为整数),则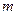 叫做离实数
叫做离实数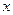 最近的整数,记作
最近的整数,记作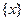 ,即
,即 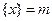 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数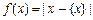 的四个命题:
的四个命题:
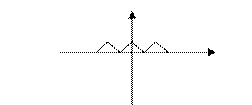
①函数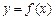 的定义域是R,值域是[0,
的定义域是R,值域是[0,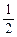 ];
];
②函数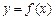 的图像关于直线
的图像关于直线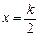 (k∈Z)对称;
(k∈Z)对称;
③函数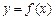 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④函数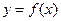 在
在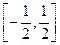 上是增函数;
上是增函数;
则其中真命题是__
相关知识点
推荐套卷
给出定义:若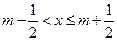 (其中
(其中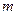 为整数),则
为整数),则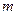 叫做离实数
叫做离实数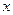 最近的整数,记作
最近的整数,记作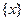 ,即
,即 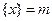 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数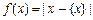 的四个命题:
的四个命题:

①函数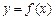 的定义域是R,值域是[0,
的定义域是R,值域是[0,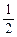 ];
];
②函数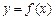 的图像关于直线
的图像关于直线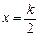 (k∈Z)对称;
(k∈Z)对称;
③函数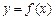 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④函数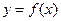 在
在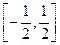 上是增函数;
上是增函数;
则其中真命题是__