(本小题满分12分)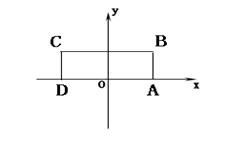
如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足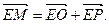 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;
(Ⅱ)已知点F(0,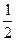 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且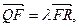 求实数
求实数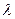 的取值范围.
的取值范围.
推荐套卷
(本小题满分12分)
如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足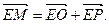 (Ⅰ)求点M的轨迹方程;
(Ⅰ)求点M的轨迹方程;
(Ⅱ)已知点F(0,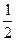 ),过点F的直线l与点M的轨迹相交于Q、R两点,且
),过点F的直线l与点M的轨迹相交于Q、R两点,且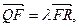 求实数
求实数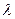 的取值范围.
的取值范围.