(本小题满分14分)已知函数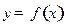 满足:
满足: ;(1)分别写出
;(1)分别写出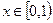 时
时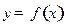 的解析式
的解析式 和
和 时
时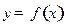 的解析式
的解析式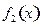 ;并猜想
;并猜想 时
时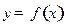 的解析式
的解析式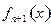 (用
(用 和
和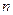 表示)(不必证明)(2)当
表示)(不必证明)(2)当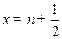
 时,
时,
 的图象上有点列
的图象上有点列 和点列
和点列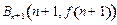 ,线段
,线段 与线段
与线段 的交点
的交点 ,求点
,求点 的坐标
的坐标 ;
;
(3)在前面(1)(2)的基础上,请你提出一个点列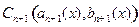 的问题,并进行研究,并写下你研究的过程
的问题,并进行研究,并写下你研究的过程
推荐套卷
(本小题满分14分)已知函数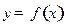 满足:
满足: ;(1)分别写出
;(1)分别写出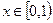 时
时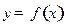 的解析式
的解析式 和
和 时
时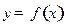 的解析式
的解析式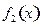 ;并猜想
;并猜想 时
时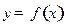 的解析式
的解析式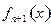 (用
(用 和
和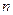 表示)(不必证明)(2)当
表示)(不必证明)(2)当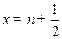
 时,
时,
 的图象上有点列
的图象上有点列 和点列
和点列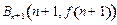 ,线段
,线段 与线段
与线段 的交点
的交点 ,求点
,求点 的坐标
的坐标 ;
;
(3)在前面(1)(2)的基础上,请你提出一个点列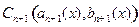 的问题,并进行研究,并写下你研究的过程
的问题,并进行研究,并写下你研究的过程