北京市东城区高一下学期期末考试数学
(本题9分)给出下面的数表序列:
| 表1 |
表2 |
表3 |
… |
| 1 |
1 3 |
1 3 5 |
|
| |
4 |
4 8 |
|
| |
|
12 |
|
其中表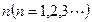 有
有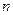 行,第1行的
行,第1行的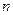 个数
个数 是1,3,5,…,
是1,3,5,…,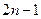 ,从第2行起,每行中的每个数都等于它肩上的两数之和。
,从第2行起,每行中的每个数都等于它肩上的两数之和。
(1)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表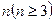 (不要求证明)
(不要求证明)
(2)每个数表中最后一行都只有一个数,它们构成数列1,4,12,…,记此数列为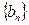 ,求数列
,求数列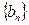 的前
的前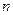 项和
项和
来源:20102011年北京市东城区高一下学期期末考试数学
若 ,
, ,则下列不等式对一切满足条件的
,则下列不等式对一切满足条件的 恒
恒 成立的是______________(写出所有正确命题的编号)。
成立的是______________(写出所有正确命题的编号)。
① ; ②
; ② ;
;  ③
③ ;
;
④ ⑤
⑤ 。
。
来源:20102011年北京市东城区高一下学期期末考试数学
将函数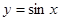 的图象上所有的点向右平移
的图象上所有的点向右平移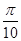 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是
A.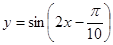 |
B.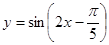 |
C.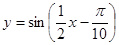 |
D.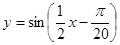 |
来源:20102011年北京市东城区高一下学期期末考试数学
如图所示,动物园要围成四间相同面积的长方形虎笼,一面可利用原有的墙,其它各面用钢筋网围成。现有36m长的钢筋网材料,则可围成的每间虎笼面积最大为_________m2。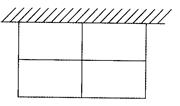
来源:20102011年北京市东城区高一下学期期末考试数学
已知 是
是 内的一点,且
内的一点,且 。定义:
。定义:
 ,其中
,其中 分别为
分别为 的面积,若
的面积,若
 ,则
,则 的最小值为______________________,此时
的最小值为______________________,此时 __________________。
__________________。
来源:20102011年北京市东城区高一下学期期末考试数学
(本题9分)甲袋中有3只白球、7只红球、1 5只黑球;乙袋中有10只白球、6只红球、9只黑球。
5只黑球;乙袋中有10只白球、6只红球、9只黑球。
(1)从甲袋中任取一球,求取到白球的概率;
(2)从两袋中各取一球,求两球颜色相同的概率;
(3)从两袋中各取一球,求两球颜色不同的概率。
来源:20102011年北京市东城区高一下学期期末考试数学
(本题9分)在平面直角坐标系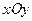 中,点
中,点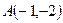 、
、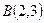 、
、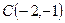 。
。
(1)求以线段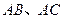 为邻边的平行四边形两条对角线的长;
为邻边的平行四边形两条对角线的长;
(2)当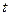 为何值时,
为何值时,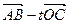 与
与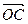 垂直;
垂直;
(3)当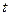 为何值时,
为何值时,
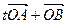 与
与 平行,平行时它们是同向还是反向。
平行,平行时它们是同向还是反向。
来源:20102011年北京市东城区高一下学期期末考试数学
(本题8分)已知等差数列 满足:
满足: ,
, 的前
的前 项和为
项和为 。
。
(1)求 及
及 ;
;
(2)令 (其中
(其中 为常数,且
为常数,且 ),求证数列
),求证数列 为等比数列。
为等比数列。
来源:20102011年北京市东城区高一下学期期末考试数学
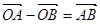
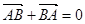
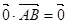
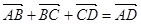
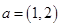 ,
,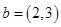 ,
,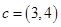 ,且
,且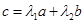 ,则
,则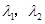 的值分别为
的值分别为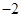 ,1
,1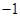 ,2
,2 ,且
,且 在第三象限,则
在第三象限,则 的值为
的值为



 和
和 同时成立的充要条件是
同时成立的充要条件是



 ,
, ,
, 是
是 上的三等分点,则
上的三等分点,则 的值为
的值为




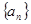 中,各项都是正数,且
中,各项都是正数,且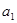 ,
,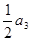 ,
,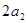 成等差数列,则
成等差数列,则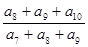 的值为
的值为
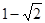
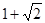
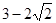
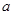 ,使得方程
,使得方程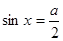 在
在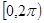 上有两个不相等的实数根
上有两个不相等的实数根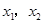 ,则
,则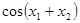 的值为
的值为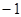
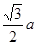
 中,内角
中,内角 的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则 的值为
的值为 区间
区间 上随机取一个数
上随机取一个数 ,则
,则 的概率为____________。
的概率为____________。 中,
中, ,
, ,前
,前 项和为
项和为 ,则
,则 =_______。
=_______。 。则
。则 ___________。
___________。 中,角
中,角 所对的边
所对的边 分别为
分别为 ,已知
,已知 。
。
 的值;
的值; ,
, 时,求
时,求 及
及 的长。
的长。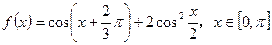 。
。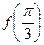 的值;
的值;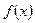 的最小值及
的最小值及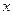 的集合;(3)求
的集合;(3)求 的最小正周期为
的最小正周期为



 粤公网安备 44130202000953号
粤公网安备 44130202000953号