广西省春季学期期中水平测试卷八年级数学
(本小题满分7分)
(1)(2)解方程:解不等式组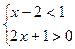
(2)如图,斜坡AC的坡度(坡比)为1: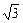 ,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.
,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度. 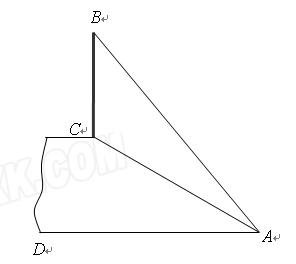
(本小题满分8分)
某社区从不同住宅楼中随机选取了200名居民,调查社区居民双休日的学习状况,并将得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2).
(1)在这个调查中,200名居民双休日在家学习的有____________人;
(2)在这个调查中,在图书馆等场所学习的居民学习时间的平均数和众数分别是多少?
(3)估计该社区2 000名居民双休日学习时间不少于4小时的人数.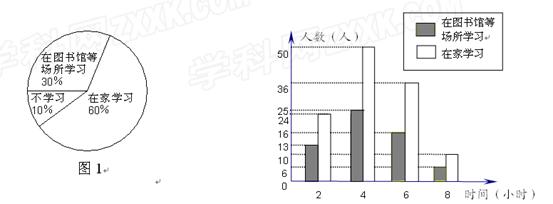
(本小题满分8分)
日本在地震后,核电站出现严重的核泄漏事故,为了防止民众受到更多的核辐射,我国某医疗公司主动承担了为日本福田地区生产2万套防辐射衣服的任务,计划10天完成,在生产2天后,日本的核辐射危机加重了,所以需公司提前完成任务,于是公司从其他部门抽调了50名工人参加生产,同时通过技术革新等手段使每位工人的工作效率比原计划提高了25%,结果提前2天完成了生产任务。求该公司原计划安排多少名工人生产防 辐射衣服?
辐射衣服?
(本小题满分9分)
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数 (x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
(本小题满分9分)
在 中,
中,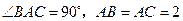 ,点
,点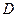 在
在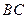 所在的直线上运动,作
所在的直线上运动,作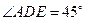 (
(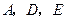 按逆时针方向).
按逆时针方向).
(1)如图1,若点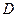 在线段
在线段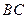 上运动,
上运动,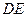 交
交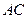 于
于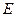 .
.
①问△ABD与△DCE相似吗?为什么?
②当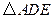 是等腰三角形时,求
是等腰三角形时,求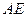 的长.
的长.
(2)① 如图2,若点
如图2,若点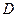 在
在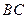 的延长线上运动,
的延长线上运动,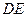 的反向延长线与
的反向延长线与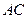 的延长线相交于点
的延长线相交于点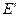 ,是否存在点
,是否存在点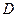 ,使
,使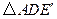 是等腰三角形?若存在,写出所有点
是等腰三角形?若存在,写出所有点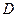 的位置;若不存在,请简要说明理由;
的位置;若不存在,请简要说明理由;
②如图3,若点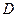 在
在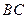 的反向延长线上运动,是否存在点
的反向延长线上运动,是否存在点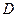 ,使
,使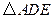 是等腰三角形?若存在,写出所有点
是等腰三角形?若存在,写出所有点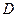 的位置;若不存在,请简要说明理由.
的位置;若不存在,请简要说明理由.
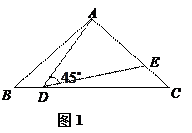
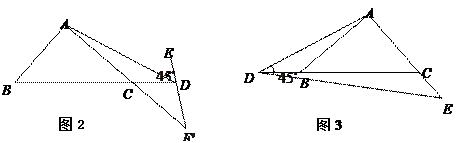
(本小题满分9分)
如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.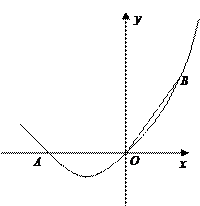
在某次聚会上,每两人都握了一次手,所有人共握手10次,设有x人参加这次聚会,则列出方程正确的是( ).
A. |
B. |
C. |
D. |
下列事件中是必然事件的是
A.一个直角三角形的两个锐角分别是 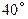 和 和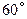 |
B.抛掷一 枚硬币,落地后正面朝上 枚硬币,落地后正面朝上 |
C.当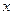 是实数时, 是实数时,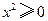 |
D.长为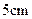 、 、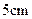 、 、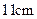 的三条线段能围成一个三 的三条线段能围成一个三 角形 角形 |
已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列
三个结论:①a<0;②a+b+c>0;③-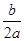 >0.其中正确的结论有( )
>0.其中正确的结论有( )
| A.只有① | B.①② | C.①③ | D.①②③ |
如图,点P(3a,a)是反比例函y=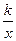 (k>0)与⊙O的一个交点,图中阴影部
(k>0)与⊙O的一个交点,图中阴影部
分的面积为10π,则反比例函数的解析式为( )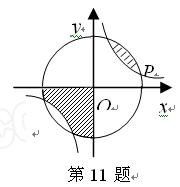
A.y = =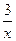 |
B.y=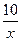 |
C.y = =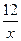  |
D.y=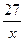 |
若用半径为20cm,圆心角为 的扇形铁皮,卷成一个圆锥容器的侧面(接缝忽略不计),则这个圆锥容器的底面半径是________cm.
的扇形铁皮,卷成一个圆锥容器的侧面(接缝忽略不计),则这个圆锥容器的底面半径是________cm.
某同学利用描点法画二次函数 的图象时,列出的部分数据如下表:
的图象时,列出的部分数据如下表:
| x |
0 |
1 |
2 |
3 |
4 |
| y |
3 |
0 |
 |
0 |
3 |
经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解析式:____________________________.
如图,以直角三角形的三边为边向三角形外作正方形,已知甲、乙两个正方形的面积分别为4、6,则丙正方形的面积为______。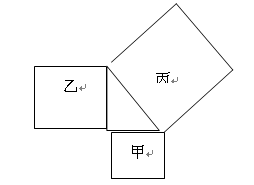
观察下面几组勾股数,并寻找规律:① 3, 4, 5;② 5,12,13;③ 7,24,25;④ 9,40,41;……请你写出有以上规律的第⑤组勾股数: 。
对于反比例函数 ,下列说法不正确的是( )
,下列说法不正确的是( )
A.点 在它的图象上 在它的图象上 |
| B.它的图象在第一、三象限 |
C.当 时, 时, 随 随 的增大而增大 的增大而增大 |
D.当 时, 时, 随 随 的增大而减小 的增大而减小 |
把分式 中的分子分母的x、y都同时扩大为原来的2倍,
中的分子分母的x、y都同时扩大为原来的2倍,
那么分式的值将是原分式值的( )
| A.2倍 | B.4倍 | C.一半 | D.不变 |
已知:如图,AB=3,AC=4,AB⊥AC,BD=12,CD=13,(1)求BC的长度;(2)证明:BC⊥BD.
某公司现要装配30台机器,在装配好6台以后,采用了新的技术,每天的工作效率提高了一倍,结果共用了3天完成任务,问原来每天装配机器有多少台?
(8分)在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C
与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,
如图13所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公
路AB段是否有危险,是否需要暂时封锁? 请通过计算进行说明。
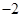 的倒数是( ).
的倒数是( ).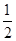
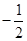
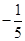
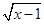 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
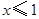
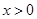
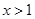





 和
和 的半径分别是3cm和5cm,若
的半径分别是3cm和5cm,若 1cm,则
1cm,则
 、
、 是一次函数
是一次函数 图象上不同的两点,若
图象上不同的两点,若 ,则( ).
,则( ).



 ________.
________. 有两个相等的实数根,那么a=________.
有两个相等的实数根,那么a=________.
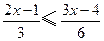 ,
, 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.
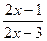 有意义。
有意义。 =" _________" 。
=" _________" 。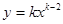 是反比例函数,那么k= 。
是反比例函数,那么k= 。 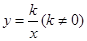 的图像经过点P(-2,-1),则该反比例函数的解析
的图像经过点P(-2,-1),则该反比例函数的解析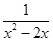 与
与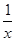 的最简公分母是__ ____。
的最简公分母是__ ____。  、
、 、
、 、
、 中,分式的个数有( )
中,分式的个数有( ) 的值是0,则x的值为( )
的值是0,则x的值为( )



 的三边长分别为5,13,12,则
的三边长分别为5,13,12,则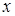 的方程
的方程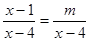 无解,则
无解,则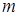 的值为( )
的值为( )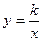 (k<0)在同一坐标系中,图象只能是下图中的( )
(k<0)在同一坐标系中,图象只能是下图中的( )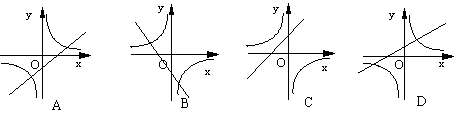


 与
与 -3成反比例,且当
-3成反比例,且当 时,求
时,求

 时,求点P的坐标。
时,求点P的坐标。 粤公网安备 44130202000953号
粤公网安备 44130202000953号