北京市顺义区高三第二次统练理科数学试卷
如图所示,一个空间几何体的正视图和左视图都是边长为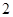 的正方形,俯视图是一个直径为
的正方形,俯视图是一个直径为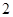 的圆,那么这个几何体的侧面积为
的圆,那么这个几何体的侧面积为
A. |
B. |
C. |
D. |
来源:2014届北京市顺义区高三第二次统练理科数学试卷
已知函数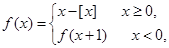 其中
其中 表示不超过
表示不超过 的最大整数,(如
的最大整数,(如 ,
, ,
, ).若直线
).若直线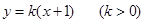 与函数
与函数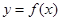 的图象恰有三个不同的交点,则实数
的图象恰有三个不同的交点,则实数 的取值范围是
的取值范围是
A.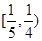 |
B.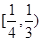 |
C.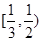 |
D.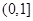 |
来源:2014届北京市顺义区高三第二次统练理科数学试卷
对甲、乙、丙、丁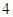 人分配
人分配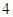 项不同的工作 A、B、C、D,每人一项,其中甲不能承担A项工作,那么不同的工作分配方案有
项不同的工作 A、B、C、D,每人一项,其中甲不能承担A项工作,那么不同的工作分配方案有 种.(用数字作答)
种.(用数字作答)
来源:2014届北京市顺义区高三第二次统练理科数学试卷
甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于 分的次数为
分的次数为 ,求
,求 的分布列和数学期望
的分布列和数学期望 ..
..
来源:2014届北京市顺义区高三第二次统练理科数学试卷
如图:在四棱锥 中,底面
中,底面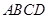 是正方形,
是正方形,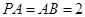 ,
, ,点
,点 在
在 上,且
上,且 .
.
(1)求证: 平面
平面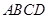 ;
;
(2)求二面角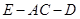 的余弦值;
的余弦值;
(3)证明:在线段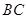 上存在点
上存在点 ,使
,使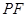 ∥平面
∥平面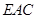 ,并求
,并求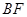 的长.
的长.
来源:2014届北京市顺义区高三第二次统练理科数学试卷
已知函数 ,其
,其 中为常数,
中为常数, .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)是否存在实数 ,使
,使 的极大值为
的极大值为 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
来源:2014届北京市顺义区高三第二次统练理科数学试卷
已知椭圆 的两个焦点分别为
的两个焦点分别为 和
和 ,离心率
,离心率 .
.
(1)求椭圆 的方程;
的方程;
(2)设直线 (
( )与椭圆
)与椭圆 交于
交于 、
、 两点,线段
两点,线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,当
,当 变化时,求
变化时,求 面积的最大值.
面积的最大值.
来源:2014届北京市顺义区高三第二次统练理科数学试卷
 等于
等于



 ,
, ,
, ,则
,则



 ,
, ,若
,若 与
与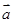 垂直,则实数
垂直,则实数
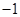

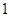

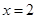 ,则输出
,则输出 的值是 ( )
的值是 ( )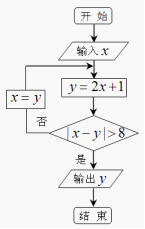
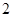



 (
( ),与抛物线
),与抛物线 的准线交于
的准线交于 两点,
两点, 为坐标原点,若
为坐标原点,若 的面积等于
的面积等于 ,则
,则



 到极轴的距离是
到极轴的距离是
 的各项均为正数,若
的各项均为正数,若 ,
, ,则
,则 此数列的其前
此数列的其前 项和
项和
 是圆
是圆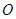 的直径,
的直径,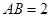 ,
, 为圆
为圆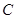 .若
.若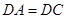 ,则
,则

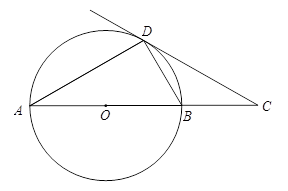
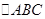 中,角
中,角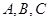 所对的边分别为
所对的边分别为 .若
.若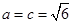 ,
, ,
,

 在由不等式
在由不等式 确定的平面区域内,则点
确定的平面区域内,则点 所在的平面区域面积是
所在的平面区域面积是
 的图象过点
的图象过点 .
.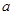 的值;
的值; 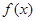 的最小正周期及最大值.
的最小正周期及最大值. ,
,
 :对任意的
:对任意的
 ,
, 至少有一个属于
至少有一个属于 .
. 与
与 是否具有性质
是否具有性质 ;
; ;
; 或
或 时集合
时集合 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号