人教A版高中数学选修4-5课时提升2-2练习卷
命题“任意多面体的面至少有一个是三角形或四边形或五边形”的结论的否定形式是 ( )
| A.任意多面体没有一个是三角形或四边形或五边形的面 |
| B.任意多面体没有一个是三角形的面 |
| C.任意多面体没有一个是四边形的面 |
| D.任意多面体没有一个是五边形的面 |
设x,y,z都是正实数,a=x+ ,b=y+
,b=y+ ,c=z+
,c=z+ ,则a,b,c三个数 ( )
,则a,b,c三个数 ( )
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
设x>0,y>0,M=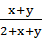 ,N=
,N=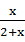 +
+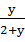 ,则M,N的大小关系
,则M,N的大小关系
是 ( )
| A.M>N | B.M<N |
| C.M=N | D.不确定 |
a,b,c不全为零等价为 ( )
| A.a,b,c均不为0 |
| B.a,b,c中至多有一个为0 |
| C.a,b,c中至少有一个为0 |
| D.a,b,c中至少有一个不为0 |
设a,b,c是正数,P=a+b-c,Q=b+c-a,R=c+a-b,则“P·Q·R>0”是“P,Q,R同时大于零”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若a,b∈R,且a2+b2=10,则a-b的取值范围是 ( )
A. |
B. |
C. |
D. |
用反证法证明命题“若ax2-(a+b)x+ab≠0,则x≠a且x≠b”时应假设 .
在△ABC中,若AB=AC,P是△ABC内一点,∠APB>∠APC,求证:∠BAP<∠CAP,用反证法证明时应分:假设 和 两类.
关于复数z的方程z2-(a+i)z-(i+2)=0(a∈R),证明对任意的实数a,原方程不可能有纯虚根.
设m>n,n∈N+,x>1,a=(lgx)m+(lgx)-m,b=(lgx)n+(lgx)-n,则a与b的大小关系为
( )
| A.a≥b |
| B.a≤b |
| C.与x的值有关,大小不定 |
| D.以上都不正确 |
已知a>b>c>0,A=a2ab2bc2c,B=ab+cbc+aca+b,则A与B的大小关系是 ( )
| A.A>B | B.A<B |
| C.A=B | D.不确定 |
使不等式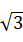 +
+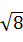 >1+
>1+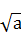 成立的正整数a的最大值
成立的正整数a的最大值
是 ( )
| A.10 | B.11 | C.12 | D.13 |
已知b>a>0,且a+b=1,则 ( )
A.2ab< < <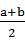 <b <b |
B.2ab<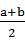 < < <b <b |
C. <2ab< <2ab<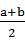 <b <b |
D.2ab<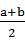 <b< <b< |
已知实数a,b,c满足b+c=6-4a+3a2,c-b=4-4a+a2,则a,b,c的大小关系
是 ( )
| A.a>c≥b | B.c≥b>a |
| C.c>b>a | D.a>c>b |
已知正整数a,b满足4a+b=30,则使得 +
+ 取最小值时的实数对(a,b)
取最小值时的实数对(a,b)
是 ( )
| A.(5,10) | B.(6,6) |
| C.(10,5) | D.(7,2) |
已知△ABC中,∠C=90°,则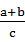 的取值范围是 ( )
的取值范围是 ( )
| A.(0,2) | B.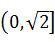 |
C. |
D.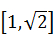 |
若实数a,b满足0<a<b且a+b=1,则下列四个数中最大的是 ( )
A. |
B.a2+b2 | C.2ab | D.a |
设a,b,c,d∈R,若a+d=b+c,且|a-d|<|b-c|,则有 ( )
| A.ad=bc | B.ad<bc |
| C.ad>bc | D.ad≤bc |
在△ABC中,A,B,C分别为a,b,c所对的角,且a,b,c成等差数列,则B满足的条件是 ( )
A.0<B≤ |
B.0<B≤ |
C.0<B≤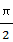 |
D.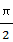 <B<π <B<π |
已知a,b为非零实数,则使不等式: +
+ ≤-2成立的一个充分而不必要条件
≤-2成立的一个充分而不必要条件
是 ( )
| A.ab>0 | B.ab<0 |
| C.a>0,b<0 | D.a>0,b>0 |
若a>b>c>0,n1= ,n2=
,n2= ,n3=
,n3= ,则n1n2,n2n3,
,则n1n2,n2n3, ,
, 中的最小的一个是 .
中的最小的一个是 .
若0<a<2,0<b<2,0<c<2,求证:(2-a)b,(2-b)c,(2-c)a不能同时大于1.
已知数列{an}满足:a1= ,
,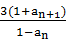 =
=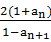 ,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=
,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn= -
- (n≥1,n∈N+).
(n≥1,n∈N+).
(1)求数列{an},{bn}的通项公式.
(2)证明:数列{bn}中的任意三项不可能成等差数列.
 +
+ +
+ +…+
+…+ <2.
<2. +
+ +…+
+…+ <
< .
. =
=

 =x-y,则x的取值范围是 .
=x-y,则x的取值范围是 .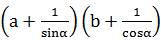 ,N=(
,N=(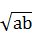 +
+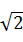 )2,则M,N的大小关系是 .
)2,则M,N的大小关系是 . +b
+b >a
>a ,
, ,
, 也可以构成一个三角形.
也可以构成一个三角形. <1,
<1, <1,求证:
<1,求证: +
+ ≥
≥ .
.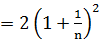 ·an(n∈N+).
·an(n∈N+).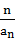 ,求证:c1+c2+c3+…+cn<
,求证:c1+c2+c3+…+cn< .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号