湖北省天门市高三天模拟理科数学试题
设集合M={ x | x2+3x+2<0},集合N={ x | ≤4},则M∪N为
≤4},则M∪N为
| A.{x | x≥-2} | B.{ x | x>-1} | C.{ x | x<-1} | D.{ x | x≤-2} |
已知x,y∈R,i为虚数单位,且(x-2)i-y=1+i,则(1+i)x+y的值为
| A.4 | B.-4 | C.4+4i | D.2i |
设g(x)是函数f(x)=ln(x+1)+2x的导函数,若函数g(x)按向量a平移后得到函数y= ,则向量a等于
,则向量a等于
| A.(1,2) | B.(-1,-2) | C.(-2,-1) | D.(2,1) |
平面直角坐标系中,点(3,t)和(2t,4)分别在顶点为原点,始边为x轴的非负半轴的角 ,
, 的终边上,则t的值为
的终边上,则t的值为
| A.±6或±1 | B.6或1 | C.6 | D.1 |
在抛物线y2=4x上有两点A,B,点F是抛物线的焦点,O为坐标原点,若 +2
+2 +3
+3 =0,则直线AB与x轴的交点的横坐标为
=0,则直线AB与x轴的交点的横坐标为
A. |
B. 1 1 |
C.6 | D. |
已知O为△ABC的外心,AB=2,AC=1,∠BAC=120°,设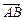 =a,
=a,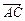 =b,
=b, =
=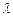 1a+
1a+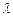 2b,则
2b,则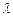 1+
1+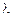 2=
2=
如图∠C=90°,AC=BC,M,N分别为BC和A B的中点,沿直线MN将△BMN折起,使二面角
B的中点,沿直线MN将△BMN折起,使二面角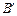 -MN-B为60°,则斜线
-MN-B为60°,则斜线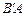 与平面ABC所成角的正切值为 .
与平面ABC所成角的正切值为 .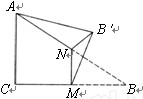
已知函数f(x)=ax2+bx+c(a≠0),且f(x)=x无实根,下列命题中:
(1)方程f [f (x)]=x一定无实根;
(2)若a>0,则不等式f [f (x)]>x对一切实数x都成立;
(3)若a<0,则必存在实数x0,使f [f (x0)]>x0;
(4)若a+b+c=0,则不等式f [f (x)]<x对一切x都成立;
正确的序号有 . 
已知△ABC的周长为6,角A,B,C所对的边a,b,c成等比数列
(1)求角B及边b的最大值;
(2)设△ABC的面积为S,求S+ 最大值
最大值
某工厂2010年第三季度生产的A,B,C,D四种型号的产品产量用条形图形表示如图,现用分层抽样的方法从中选取50件样品参加2011年4月份的一个展销会。
(1)A,B,C,D型号的产品各抽取多少件?
(2)从50件样品随机地抽取2件,求这2件产品恰好是不同型号产品的概率。
(3)从A,C型号的样品中随机地抽取3件,用ξ表示抽取A型号的产品件数,求ξ的分布列和数学期望
如图,四棱锥P-ABCD的底面为矩形,侧棱PD垂直于底面,PD=DC=2BC,E为棱PC上的点,且平面BDE⊥平面PBC.
(1)求证:E为PC的中点;
(2)求二面角A-BD-E的大小.
已知函数f(x)=x3+3ax-1的导函数f ′ (x),g(x)=f ′(x)-ax-3.
(1)当a=-2时,求函数f(x)的单调区间;
(2)若对满足-1≤a≤1的一切a的值,都有g(x)<0,求实数x的取值范围;
(3)若x·g ′(x)+lnx>0对一切x≥2恒成立,求实数a的取值范围.
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率 .
.
(1)求证: ,
, ,
, 依次成等差数列;
依次成等差数列;
(2)若F( ,0),求直线AB在双曲线上所截得的弦CD的长度.
,0),求直线AB在双曲线上所截得的弦CD的长度.
 ,则球的体积为
,则球的体积为



 的左、右焦点,点P在椭圆上运动,则
的左、右焦点,点P在椭圆上运动,则 的最大值是
的最大值是 (n∈N﹡),则a2011等于
(n∈N﹡),则a2011等于


 <
< ,则函数y=
,则函数y= 的值域为
的值域为 )
) )
)
 ,则点集M所覆盖的平面图形的面积为
,则点集M所覆盖的平面图形的面积为


 有关
有关 的展开式中,常数项为 .(用数字作答)
的展开式中,常数项为 .(用数字作答) 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) . ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值; ,证明:
,证明: ( n∈N﹡).
( n∈N﹡). 粤公网安备 44130202000953号
粤公网安备 44130202000953号