已知数列{an},且x= 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
(1)求数列{an}的通项公式;
(2)记bn=2(1-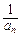 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
(3)若cn=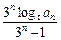 ,证明:
,证明: ( n∈N﹡).
( n∈N﹡).
推荐套卷
已知数列{an},且x= 是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的
是函数f(x)=an-1x3-3[(t+1)an-an+1] x+1(n≥2)的 一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
一个极值点.数列{an}中a1=t,a2=t2(t>0且t≠1) .
(1)求数列{an}的通项公式;
(2)记bn=2(1-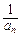 ),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2010的n的最小值;
(3)若cn=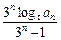 ,证明:
,证明: ( n∈N﹡).
( n∈N﹡).