北京市海淀区高三第二学期第二次模拟(理科)数学题
某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:
| |
|
|
|
|
甲 |
|
乙 |
|
|
|
|
|
| |
|
|
9 |
8 |
8 |
1 |
7 |
7 |
9 |
9 |
|
|
| |
|
|
6 |
1 |
0 |
2 |
2 |
5 |
6 |
7 |
9 |
9 |
| |
|
5 |
3 |
2 |
0 |
3 |
0 |
2 |
3 |
|
|
|
| |
|
|
7 |
1 |
0 |
4 |
|
|
|
|
|
|
根据上图,对这两名运动员的成绩进行比较,下列四个结论中,不正确的是
| A.甲运动员得分的极差大于乙运动员得分的极差 |
| B.甲运动员得分的的中位数大于乙运动员得分的的中位数 |
| C.甲运动员的得分平均值大于乙运动员的得分平均值 |
| D.甲运动员的成绩比乙运动员的成绩稳定 |
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
若椭圆 :
: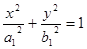 (
(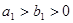 )和椭圆
)和椭圆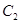 :
: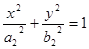 (
( )
)
的焦点相同且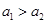 .给出如下四个结论:
.给出如下四个结论:
椭圆 和椭圆
和椭圆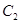 一定没有公共点; ②
一定没有公共点; ② ;
;
③ 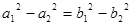 ; ④
; ④ .
.
其中,所有正确结论的序号是
| A.②③④ | B.①③④ | C.①②④ | D.①②③ |
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
在一个正方体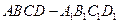 中,
中,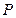 为正方形
为正方形 四边上的动点,
四边上的动点, 为底面正方形
为底面正方形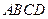 的中心,
的中心, 分别为
分别为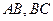 中点,点
中点,点 为平面
为平面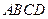 内一点,线段
内一点,线段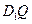 与
与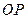 互相平分,则满足
互相平分,则满足 的实数
的实数 的值有
的值有 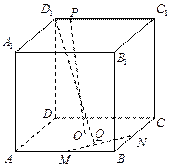
| A.0个 | B. 1个 | C.2个 | D. 3个 |
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
已知函数
(1)判断下列三个命题的真假:
① 是偶函数;②
是偶函数;② ;③当
;③当 时,
时, 取得极小值.
取得极小值.
其中真命题有____________________;(写出所有真命题的序号)
(2)满足 的正整数
的正整数 的最小值为___________.
的最小值为___________.
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.
(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率;
(Ⅱ) 用 表示4名乘客在第4层下电梯的人数,求
表示4名乘客在第4层下电梯的人数,求 的分布列和数学期望.
的分布列和数学期望.
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
如图,四棱锥 的底面是直角梯形,
的底面是直角梯形, ,
, ,
, 和
和 是两个边长为
是两个边长为 的正三角形,
的正三角形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
在平面直角坐标系 中,设点
中,设点 ,以线段
,以线段 为直径的圆经过原点
为直径的圆经过原点 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 与轨迹
与轨迹 交于两点
交于两点 ,点
,点 关于
关于 轴的对称点为
轴的对称点为 ,试判断直线
,试判断直线 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.
来源:2011届北京市海淀区高三第二学期第二次模拟(理科)数学题
 在复平面上对应的点的坐标是
在复平面上对应的点的坐标是



 集合
集合 ,
, ,下图中阴影部分所表示的集合为
,下图中阴影部分所表示的集合为
 B.
B.  C.
C.  D.
D. 
 的零点所在区间
的零点所在区间



 的参数方程为
的参数方程为 ,则直线
,则直线



 在不等式组
在不等式组 表示的平面区域内,则
表示的平面区域内,则 的最大值为_______.
的最大值为_______. ,则输出
,则输出 的值为 .
的值为 .
 ,其中
,其中 ,则实数
,则实数 的值为 ;
的值为 ;  的值为 .
的值为 . 的弦
的弦 交半径
交半径 于点
于点 ,若
,若 ,
, ,且
,且 的长为 .
的长为 .
 满足
满足 ,
,
 ,记数列
,记数列 项和的最大值为
项和的最大值为 ,则
,则 .
.
 的最小正周期为
的最小正周期为 .
. 的值;
的值; 的单调区间及其图象的对称轴方程.
的单调区间及其图象的对称轴方程. 
 .
. .
. 时,求曲线
时,求曲线 在
在 处的切线方程(
处的切线方程( );
); 的单调区间.
的单调区间. ,若满足
,若满足 ,则称数列
,则称数列 为“0-1数列”.定义变换
为“0-1数列”.定义变换 ,
, :1,0,1,则
:1,0,1,则 设
设 是“0-1数列”,令
是“0-1数列”,令
 .
. :
: 求数列
求数列 ;
; 共有10项,则数列
共有10项,则数列 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由; 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为 ,
, .求
.求 的表达式.
的表达式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号