高考数学总复习考点引领+技巧点拨第三章第4课时练习卷
化简:tan(18°-x)tan(12°+x)+ [tan(18°-x)+tan(12°+x)]=________.
[tan(18°-x)+tan(12°+x)]=________.
来源:2014届高考数学总复习考点引领+技巧点拨第三章第4课时练习卷
已知α、β均为锐角,且sinα=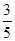 ,tan(α-β)=-
,tan(α-β)=- .
.
(1) 求sin(α-β)的值;
(2) 求cosβ的值.
来源:2014届高考数学总复习考点引领+技巧点拨第三章第4课时练习卷
已知角φ的终边经过点P(1,-2),函数f(x)=sin(ωx+φ)(ω>0)图象的相邻两条对称轴之间的距离为 ,则f
,则f =__________.
=__________.
来源:2014届高考数学总复习考点引领+技巧点拨第三章第4课时练习卷
函数f(x)=sin2x·sin -cos2x·cos
-cos2x·cos 在
在 上的单调递增区间为_________.
上的单调递增区间为_________.
来源:2014届高考数学总复习考点引领+技巧点拨第三章第4课时练习卷
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为 、
、 .求:
.求:
(1) tan(α+β)的值;
(2) α+2β的值.
来源:2014届高考数学总复习考点引领+技巧点拨第三章第4课时练习卷
 =
= ,tan
,tan  =
= ,则tan(α+β)=________.
,则tan(α+β)=________. ,α∈
,α∈ ,则cos
,则cos =__________.
=__________. =________.
=________. =________.
=________. tan20°tan40°.
tan20°tan40°. ,sinβ=
,sinβ= ,且α、β为锐角,则α+β的值为__________.
,且α、β为锐角,则α+β的值为__________. ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α< ,求β.
,求β. <α<
<α< π,cos(
π,cos( ,sin(
,sin( +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值. ,sinα=
,sinα= ,tan(α-β)=-
,tan(α-β)=- ,求cosβ的值.
,求cosβ的值.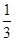 ,cos(α+β)=-
,cos(α+β)=-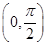 ,求cos(α-β)的值.
,求cos(α-β)的值. +sinα=-
+sinα=- ,-
,- <α<0,则cosα=__________.
<α<0,则cosα=__________. =
= ,则sinθ+cosθ=________.
,则sinθ+cosθ=________. ,则tan(α+β)=________.
,则tan(α+β)=________. +sinα=
+sinα= ,则sin
,则sin 的值为________.
的值为________. +cos
+cos ,x∈R.
,x∈R. ,cos(β+α)=-
,cos(β+α)=- ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0. 粤公网安备 44130202000953号
粤公网安备 44130202000953号