安徽省宣城市高三第二次模拟考试数学理卷
.以直角坐标系的原点为极点, 轴的正半轴为极轴建立极坐标系,并在两坐标系中取相同的长单位,曲线
轴的正半轴为极轴建立极坐标系,并在两坐标系中取相同的长单位,曲线 的参数方程为
的参数方程为 (参数
(参数 ),直线
),直线 的极坐标方程为
的极坐标方程为 .则在
.则在 上到直线
上到直线 距离分别为
距离分别为 和
和 的点共有
的点共有
| A.1个 | B.2个 | C.3个 | D.4个 |
来源:2011届广东省汕头市高三四校联考数学文卷
某工厂对100件新产品的尺寸(单位:cm)进行检测,所得数据均在
 中,其频率分布直方图如图,则在这100件新产品中,有
中,其频率分布直方图如图,则在这100件新产品中,有  件长小于15cm.
件长小于15cm.
来源:2011届广东省汕头市高三四校联考数学文卷
给出下列四个命题
①命题“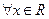 ,
, ”的否定是“
”的否定是“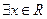 ,
, ”;
”;
②若 只有一个零点,则
只有一个零点,则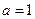 ;
;
③若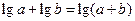 ,则
,则 的最小值为4;
的最小值为4;
④对于 任意实数
任意实数 ,有
,有 ,
,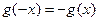 ,且当
,且当 时,
时, ,
, ,则当
,则当 时,
时, .
. 其中正确的命题有 (填所有正确的序号)
其中正确的命题有 (填所有正确的序号)
来源:2011届广东省汕头市高三四校联考数学文卷
(本小题满分12分)
某人向一目标射击,在 处射击一次击中目标的概率为
处射击一次击中目标的概率为 ,击中目标得2分;在
,击中目标得2分;在 处射击一次击中目标的概率为
处射击一次击中目标的概率为 ,击中目标得1分.若他射击三次,第一次在
,击中目标得1分.若他射击三次,第一次在 处射击,后两次都在
处射击,后两次都在 处射击,用
处射击,用 表示他3次射击后得的总分,其分布列为:
表示他3次射击后得的总分,其分布列为:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
⑴求 及的数学期望
及的数学期望 ;
;
⑵求此人3次都选择在 处向目标射击且得分高于2分的概率.
处向目标射击且得分高于2分的概率.
来源:2011届广东省汕头市高三四校联考数学文卷
(本小题满分12分)
如图,在多面体 中,四边形
中,四边形 是正方形,
是正方形, 平面
平面 ,
, ,
, ,
, ,
, ,点
,点 是
是 的中点.
的中点.
⑴求证: 平面
平面 ;
;
⑵求二面角 的余弦值.
的余弦值.
来源:2011届广东省汕头市高三四校联考数学文卷
(本小题满分12分)
已知椭圆 的右顶点为
的右顶点为 ,点
,点 在椭圆上,且它的横坐标为1,点
在椭圆上,且它的横坐标为1,点 ,且
,且 .
.
⑴求椭圆的方程;⑵若过点 的直线
的直线 与椭圆交于另一点
与椭圆交于另一点 ,若线段
,若线段 的垂直平分线经过点
的垂直平分线经过点 ,求直线
,求直线 的方程.
的方程.
来源:2011届广东省汕头市高三四校联考数学文卷
(本小题满分13分)
在数列 中,
中, ,点
,点 在直线
在直线 上,设
上,设 ,数列
,数列 是等比数列.
是等比数列.
⑴求出实数 ;
;
⑵令 ,问从第几项开始,数列
,问从第几项开始,数列 中连续20项之和为100?
中连续20项之和为100?
来源:2011届广东省汕头市高三四校联考数学文卷
 ,
, ,则
,则




 是虚数单位,复数
是虚数单位,复数 满足
满足 ,则
,则






 的离心率为
的离心率为 ,且它的两焦点到直线
,且它的两焦点到直线 的距离之和为2,则该比曲线方程是
的距离之和为2,则该比曲线方程是



 的图像可能是
的图像可能是
 中,
中, ,
, ,
, ,点
,点 在
在 边上,
边上, ,则
,则




 知不等式组
知不等式组 (
( )表示的平面区域的面积为
)表示的平面区域的面积为 ,则
,则




 ,
, ,…,
,…, 分别为
分别为 ,
, ,
, ,
, ,
, ,
, ,则输出的
,则输出的 ,
, 分别为
分别为
 ,
,
 ,
, 的八个顶点任两点连线中,随机取一直线,则该直线与平面
的八个顶点任两点连线中,随机取一直线,则该直线与平面 平行的概率为
平行的概率为



 的首项为正数,
的首项为正数, ,
, ,若对满足
,若对满足 的任意
的任意 ,
, 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是 B
B .
. C.
C. D.
D.
 的展开式中,
的展开式中, 的系数为
的系数为 
 ,则满足
,则满足 的
的 的取值范围是
的取值范围是  ,
, .
. 的最小正周期;⑵求函数
的最小正周期;⑵求函数 的最小值,并求使
的最小值,并求使 取得最小值时
取得最小值时 的取值集合.
的取值集合. .
. 在
在 处的切线方程为
处的切线方程为 ,求实数
,求实数 和
和 的值;
的值; 对任意
对任意 恒成立的充要条件是
恒成立的充要条件是 ;
; ,且对任意
,且对任意 、
、 ,都
,都 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号