上海市卢湾区高三上学期期末数学理卷
在一次招聘口试中,每位考生都要在5道备选试题
中随机地抽出3道题回答,答对其中2道题即为及格.
若一位考生只会回答5道题中的3道题,则这位考生
能够及格的概率为 .
(理)某投篮游戏规定:每轮至多投三次,直到首次命中为止.第一次就投中,得8分;第一次不中且第二次投中,得6分;前两次均不中且第三次投中,得4分;三次均不中,得0分.若某同学每次投中的概率为0.5,则他每轮 游戏的得分X的数学期望为 .
游戏的得分X的数学期望为 .
 一个调查机构就某地居民的月收入调查
一个调查机构就某地居民的月收入调查
了10000人,将所得数据分成如下六组:

相应的频率分布直方图如图所示.若按月
收入将这10000人也分成上述六组,并通
过分层抽样抽出100人作进一步调查,则 这一组中应抽出 人.
这一组中应抽出 人.
在三棱锥P—ABC中,所有棱长均相等,若M为棱
AB的中点,则PA与CM所成角的余弦值为( )
A. |
B.  |
C. |
D. |

将5,6,7,8四个数填入 中的空白处以构成三行三列方阵,若要求每一行从左到右、每一列从上到下依次增大,则满足要求的填法种数为 ( )
中的空白处以构成三行三列方阵,若要求每一行从左到右、每一列从上到下依次增大,则满足要求的填法种数为 ( )
| A.24 | B.18 | C.12 | D.6 |
已知 是单调减函数,若将方程
是单调减函数,若将方程 与
与 的解分别称为函数
的解分别称为函数 的不动点与稳定点.则“
的不动点与稳定点.则“ 是
是 的不动点”是“
的不动点”是“ 是
是 的稳定点”的( )
的稳定点”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
本题共2个小题,第1小题6分,第2小题6分.
已知 是复数,
是复数, 为实数(
为实数( 为
为 虚数单位),且
虚数单位),且 .
.
(1)求复数 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
( 本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知 ,
, ,
, 为△ABC的三个内角,向量
为△ABC的三个内角,向量 ,
, ,且
,且 .
.
(1)求 的大小;
的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是
 上一点.设
上一点.设 ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于 的函数解析式;
的函数解析式;
(2)设 ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数 (常数
(常数 .
.
(1)若 ,且
,且 ,求x的值;
,求x的值;
(2)若 ,求证函数
,求证函数 在
在 上是增函数;
上是增函数;
(3)若存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,集合
,集合 ,
, ,则
,则 .
.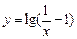 的定义域是 .
的定义域是 . 在
在 上的解集是 .
上的解集是 . 时,行列式
时,行列式 的值是 .
的值是 . …
… )的值为 .
)的值为 . 是奇函数,当
是奇函数,当 时,
时,

 ,且
,且 ,则
,则 = .
= .
 的解为
的解为 ,则大于
,则大于 的最小
的最小 的图像过点
的图像过点 ,
, ,则
,则 的值为
的值为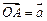 ,
,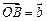 ,点
,点 …
…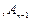 是线段AB的n
是线段AB的n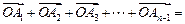 .(用
.(用 表示)
表示) 的最小正周期是 ( )
的最小正周期是 ( )



 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当 ≥0时, 有[
≥0时, 有[ ,
,  ]=
]= ,
, 
 ].
]. }是等比数列;
}是等比数列; ,求证
,求证
 ;
; ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由 粤公网安备 44130202000953号
粤公网安备 44130202000953号