本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知负数 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当 ≥0时, 有[
≥0时, 有[ ,
, 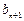 ]=
]=
[ ,
,  ];当
];当 <0时, 有[
<0时, 有[ ,
, 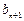 ]= [
]= [ ,
, 
 ].
].
(1)求证数列{ }是等比数列;
}是等比数列;
(2)若 ,求证
,求证
 ;
;
(3)是否存在 ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由
推荐套卷
本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知负数 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当 ≥0时, 有[
≥0时, 有[ ,
, 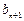 ]=
]=
[ ,
,  ];当
];当 <0时, 有[
<0时, 有[ ,
, 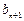 ]= [
]= [ ,
, 
 ].
].
(1)求证数列{ }是等比数列;
}是等比数列;
(2)若 ,求证
,求证
 ;
;
(3)是否存在 ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由