[浙江]2014届山东泰州市姜堰区九年级第一学期期末调研数学试卷
在统计中,样本的标准差可以反映这组数据的
| A.集中程度 | B.分布规律 | C.离散程度 | D.数值大小 |
方程x2="2" x的解是
| A.x=2 | B.x1= ,x2=0 ,x2=0 |
C.x1=2,x2=0 | D.x="0" |
如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为
A. 4cm B.6cm C. 8cm D.10cm
如图,已知AB是圆O的直径,∠BAC=32°,D为弧AC的中点,那么∠DAC的度数是
| A.25° | B.29° | C.30° | D.32° |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列四个结论
①a、b同号
②当x=1和x=3时函数值相等
③4a+b=0
④当y= 时x的值只能取0
时x的值只能取0
其中正确的个数
| A.1个 | B.2个 | C.3个 | D.4个 |
随机从甲、乙两块试验田各抽取100株麦苗测量高度(单位:cm),计算平均数和方差的结果为 =13,
=13, =13,
=13, =3.6,
=3.6, =15.8,则小麦长势比较整齐的试验田是 .
=15.8,则小麦长势比较整齐的试验田是 .
如图,⊙O的直径AB=6,CD是⊙O的弦,CD⊥AB,垂足为P,且AP∶BP=2∶1,则CD长为 .
在学校组织的实践活动中,小明同学用纸板制作了一个如图所示的圆锥模型,它的底面积半径为1,高为 ,则这个圆锥的侧面积为 .(结果保留π)
,则这个圆锥的侧面积为 .(结果保留π)
一种药品经过两次降价,药价从每盒100元调至每盒81元,则平均每次降价的百分率是____________
如图,边长为1的小正方形构成的网格中,⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为 (结果保留π)
军事演习在平坦的草原上进行,一门迫击炮发射的一发炮弹的飞行高度y(米)和飞行时间x(秒)的关系满足二次函数 ,由此可知,炮弹能命中 米远的地面目标.
,由此可知,炮弹能命中 米远的地面目标.
在平面直角坐标系中,⊙O的半径为1,点P(a,0). ⊙P的半径为2,将⊙P向左平移,当⊙P与⊙O相切时,则a的值为 .
如图,在△ABC和△DCB中,AC与BD交于点E,且AC=BD,AB=CD.
(1)求证:△ABC≌△DCB;(2)若∠AEB=70°,求∠EBC的度数.
如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
在一分钟投篮测试中,甲、乙两组同学的一次测试成绩如下:
| 成绩 |
4 |
5 |
6 |
7 |
8 |
9 |
| 甲组(人) |
1 |
2 |
4 |
2 |
1 |
5 |
| 乙组(人) |
1 |
1 |
3 |
5 |
2 |
3 |
(1)求甲、乙两组一分钟投篮测试成绩的平均数和方差;
(2)从统计学的角度看,你认为哪组同学的测试成绩较好?为什么?
如图,在□ABCD中,EF垂直平分AC交BC于E,交AD于F.
(1)求证:四边形AECF为菱形;
(2)若AC⊥CD,AB=6,BC=10,求四边形AECF的面积.
正常水位时,抛物线拱桥下的水面宽为BC=20m,水面上升3m达到该地警戒水位DE时,桥下水面宽为10m.若以BC所在直线为x轴,BC的垂直平分线为y轴,建立如图所示的平面直角坐标系.
(1)求桥孔抛物线的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没;
(3)当达到警戒水位时,一艘装有防汛器材的船,露出水面部分的宽为4m,高为0.75m,通过计算说明该船能否顺利通过此拱桥?
如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;
如图,在⊙O中,AB为⊙O的直径,AC为弦,OC=4,∠OAC=60°.

(1)求∠AOC的度数;
(2)在图(1)中,P为直径BA的延长线上一点,且 ,求证:PC为⊙O的切线.
,求证:PC为⊙O的切线.
(3)如图(2),一动点M从A点出发,在⊙O上按逆时针方向运动一周(点M不与点C重合),当 时,求动点M所经过的弧长.
时,求动点M所经过的弧长.
 有意义,则x的取值范围是
有意义,则x的取值范围是 ,则
,则 =__________
=__________ 的一个根,则
的一个根,则 的值为 .
的值为 .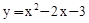 的图象如图所示,则y<0时自变量x的取值范围是 .
的图象如图所示,则y<0时自变量x的取值范围是 .
 ;
; ,求
,求 的值.
的值. ,其中
,其中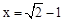 .
. (k为正整数).
(k为正整数).
 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 粤公网安备 44130202000953号
粤公网安备 44130202000953号