[四川]2014届四川省乐至县九年级上学期期末质量检测数学试卷
下列关于x的一元二次方程中,没有实数根的方程是( ).
| A.x2+4=0 | B.4x2﹣4x﹣1=0 | C.x2﹣x﹣3=0 | D.x2+2x﹣1=0 |
把ΔABC沿 轴向下平移3个单位得到
轴向下平移3个单位得到 ,如果A(2,4),则
,如果A(2,4),则 的坐标是( ).
的坐标是( ).
| A.(5,4) | B.(-1,4) | C.(2,7) | D.(2,1) |
在Rt△ABC中,已知:45°<A<90°,则下列各式成立的是( ).
| A.sinA=cosA | B.sinA>cosA | C.sinA>tanA | D.sinA<cosA |
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( ).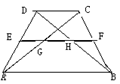
| A.AB∥EF |
| B.AB+DC=2EF |
| C.四边形AEFB和四边形ABCD相似. |
| D.EG=FH |
今年以来,某种食品不断上涨,在9月份的售价为8.1元/kg,11月份的售价为10元/kg。这种食品平均每月上涨的百分率约等于( ).
| A.15℅ | B.11℅ | C.20℅ | D.9℅ |
下列说法正确的是( ).
| A.三角形的重心是三角形三边垂直平分线的交点. |
| B.三角形的一条中位线与第三边上的中线互相平分. |
C.坡面的水平长度 与铅垂高度 与铅垂高度 的比是坡比 的比是坡比 |
| D.相似三角形对应高的比等于相似比的平方. |
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形 与矩形OABC关于点O位似,且矩形
与矩形OABC关于点O位似,且矩形 的面积等于矩形OABC面积的
的面积等于矩形OABC面积的 ,那么点B/的坐标是( ).
,那么点B/的坐标是( ).
A. |
B. |
C. 或 或 |
D. 或 或 |
如图所示,△ABC∽△DEF 其相似比为K , 则一次函数 的图像与两坐标轴围成的三角形面积是( )
的图像与两坐标轴围成的三角形面积是( )
| A.0.5 | B.4 | C.2 | D. 1 |
以下结论正确的有 .(填番号)
(1)在△ACB中,F是BC上一点,如果∠AFC=∠BAC,则

(2)在Rt△ABC中∠C=90°,若cosB= ,则
,则 .
.
(3)计算( )÷
)÷ 的结果是1+
的结果是1+ .
.
(4) 是一元二次方程,则不等式
是一元二次方程,则不等式 的解集是
的解集是 >-1.
>-1.
我县今年初中的实验考试,采用学生抽签的方式决定自己的考试内容,规定:每位考生先在物理学科三个实验题(题签分别用代码B1、B2、B3表示)中抽取一个,再在化学学科三个实验题(题签分别用代码J1、J2、J3表示)中抽取一个进行实验操作考试.如果你在看不到题签的情况下,分别随机地各抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求你抽到的题签代码的下标(例如“B1”的下表为“1”)均为奇数的概率.
如图,在正方形网格上有△ABC和△DEF.
(1)求证:△ABC∽△DEF;
(2)计算这两个三角形的周长比;
(3)根据上面的计算结果,你有何猜想?
2013年10月31日20时02分在台湾花莲县,发生6.7级地震,某地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象,已知废墟一侧地面上两探测点A、B 相距3米,探测线与地面夹角分别是30°和 60°(如图),试确定生命所在点 C 的深度。(结果精确到0.1米,参考数据: )
)
如果 分别是一元二次方程
分别是一元二次方程
 +
+
 +
+ =0(
=0( ≠0)的两根,请你解决下列问题:
≠0)的两根,请你解决下列问题:
(1)推导根与系数的关系: =-
=- ,
, =
=
(2)已知 ,
, 是方程
是方程 -4
-4 +2=0的两个实根,利用根与系数的关系求
+2=0的两个实根,利用根与系数的关系求 的值;
的值;
(3)已知sin ,cos
,cos (
( )是关于x的方程2
)是关于x的方程2 -
- 的两个根,求角
的两个根,求角 的度数.
的度数.
为了探索代数式 的最小值,
的最小值,
小张巧妙的运用了数学思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作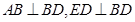 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则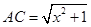 ,
,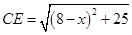 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.
(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得 的最小值等于 ,此时
的最小值等于 ,此时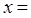 ;
;
(2)题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想?
(选填:函数思想,分类讨论思想、类比思想、数形结合思想)
(3)请你根据上述的方法和结论,试构图求出代数式 的最小值.
的最小值.
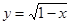 中,自变量
中,自变量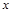 的取值范围是( ).
的取值范围是( ). 与
与 是同类二次根式,则
是同类二次根式,则 的值不可能是( ).
的值不可能是( ). ,那么
,那么 = .
= . 的结果是 .
的结果是 . (
( ≠0)的一个根是1,且
≠0)的一个根是1,且 ,则一元二次方程的另一个根是 .
,则一元二次方程的另一个根是 .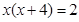
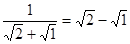 ,
,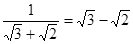 ,
,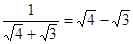 ,
,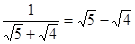 …从计算结果中找出规律,并利用这一规律计算:
…从计算结果中找出规律,并利用这一规律计算: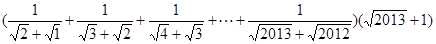

 为何值时,△BPQ为直角三角形;
为何值时,△BPQ为直角三角形; 粤公网安备 44130202000953号
粤公网安备 44130202000953号