浙江省金丽衢十二校第一次联考理科数学卷
已知 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既非充分也非必要条件 |
为了得到函数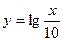 的图像,只需把函数
的图像,只需把函数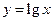 的图像上所有的点
的图像上所有的点
| A.向左平移1个单位长度 | B.向右平移1个单位长度 |
| C.向上平移1个单位长度 | D.向下平移1个单位长度 |
函数 是
是
A.最小正周期为 且在[ 且在[ ]内有且只有三个零点的函数; ]内有且只有三个零点的函数; |
B.最小正周期为 且在[ 且在[ ]内有且只有二个零点的函数; ]内有且只有二个零点的函数; |
C.最小正周期为 且在[ 且在[ ]内有且只有三个零点的函数; ]内有且只有三个零点的函数; |
D.最小正周期为 且在[ 且在[ ]内有且只有二个零点的函数. ]内有且只有二个零点的函数. |
如图,已知三棱柱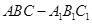 的各条棱长都相等,且
的各条棱长都相等,且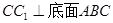 ,
, 是侧棱
是侧棱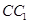 的中点,则异面直线
的中点,则异面直线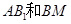 所成的角的大小是
所成的角的大小是 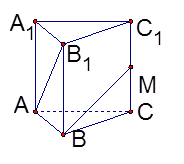
A.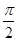 |
B. |
C.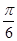 |
D. |
设第一象限内的点(x,y)满足约束条件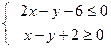 ,
,
若目标函数z=ax+by(a>0,b>0)的最大值为40,则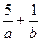 的最小值为 .
的最小值为 .
A.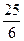 |
B.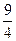 |
C.1 | D.4 |
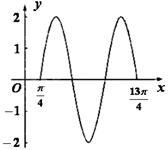
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数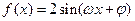 的图像,其部分图像如图所示,则
的图像,其部分图像如图所示,则
设 和
和 是抛物线
是抛物线 上的两个动点,且在
上的两个动点,且在 和
和 处的抛物线切线相互垂直,已知由
处的抛物线切线相互垂直,已知由 及抛物线
及抛物线 的顶点所成的三角形重心的轨迹也是一抛物线,记为
的顶点所成的三角形重心的轨迹也是一抛物线,记为 .对
.对 重复以上过程,又得一抛物线
重复以上过程,又得一抛物线 ,余类推.设如此得到抛物线的序列为
,余类推.设如此得到抛物线的序列为 ,
, ,
, ,若抛物线
,若抛物线 的方程为
的方程为 ,经专家计算得,
,经专家计算得, ,
,  ,
, ,
,  ,
,  .
.
则 .:Z_x
.:Z_x
已知: 直线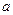 ,
,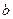 , 平面
, 平面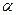 ,
, ,
,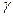 ,给出下列四个命题:
,给出下列四个命题:
①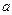 ∥
∥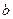 ,
,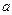 ⊥
⊥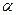 ,
,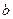 ∥
∥ ,则
,则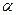 ⊥
⊥ ;
;
②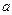 ∥
∥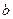 ,
, 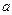 ∥
∥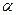 ,
,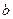 ∥
∥ ,则
,则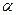 ∥
∥ ;
;
③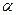 ⊥
⊥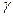 ,
,  ⊥
⊥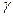 ,则
,则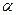 ∥
∥ ;
;
④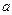 ∥
∥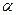 ,
,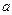 ∥
∥ ,
, 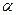 ∩
∩ =
=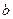 ,则
,则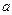 ∥
∥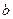 .
.
其中真命题是 (填写真命题的编号)
设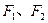 分别为双曲线
分别为双曲线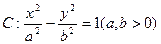 的左右焦点,
的左右焦点,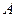 为双曲线的左顶点,以
为双曲线的左顶点,以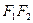 为直径的圆交双曲线某条渐近线于
为直径的圆交双曲线某条渐近线于 两点,且满足
两点,且满足 .则该双曲线的离心率为
.则该双曲线的离心率为
在△ABC 中, a,b,c分别为角A,B,C的对边,已知
中, a,b,c分别为角A,B,C的对边,已知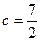 ,△ABC的面积为
,△ABC的面积为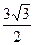 ,又
,又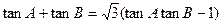 .
.
(Ⅰ)求角C的大小;
(Ⅱ)求a+b的值.
已知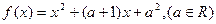 ,若
,若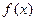 能表示成一个奇函数
能表示成一个奇函数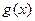 和一个偶函数
和一个偶函数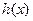 的和.
的和.
(Ⅰ)求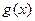 和
和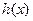 的解析式;
的解析式;
(Ⅱ)若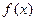 和
和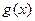 在区间
在区间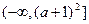 上都是减函数,求
上都是减函数,求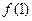 的取值范围.
的取值范围.
如图,在长方体 中,
中, ,且
,且
 .
.
(Ⅰ)求证:对任意 ,总有
,总有 ;
;
(Ⅱ)若 ,求二
,求二 面角
面角 的余弦值;
的余弦值;
(Ⅲ)是否存在 ,使得
,使得 在平面
在平面 上的射影平分
上的射影平分 ?若存在,求出
?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知椭圆 (
( )的两个焦点分别为
)的两个焦点分别为 ,点P在椭圆上,且满足
,点P在椭圆上,且满足 ,
, ,直线
,直线 与圆
与圆 相切,与椭圆相交于A,B两点.
相切,与椭圆相交于A,B两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明 为定值(O为坐标原点)
为定值(O为坐标原点)
 相切,则
相切,则 的值为
的值为 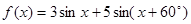 的最大值是
的最大值是  ,则方程
,则方程 表示的曲线只可能是
表示的曲线只可能是

 ,集合
,集合 ,
, ,则集合
,则集合
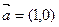 ,
,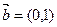 ,
,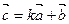 ,
, ,如果
,如果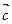 ∥
∥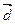 ,则
,则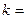
 )如右图所示,则该几何体的表面积为 _
)如右图所示,则该几何体的表面积为 _


 .
. 的单调性;
的单调性; .当
.当 时,若对任意
时,若对任意 ,
, ,使
,使 ,求实数
,求实数 的最小值
的最小值 粤公网安备 44130202000953号
粤公网安备 44130202000953号