辽宁省锦州市高三第一学期末理科数学卷
“a=1”是“函数y=cos2ax-sin2ax的最小正周期为π”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既非充分条件也不是必要条件 |
在样本的频率分布直方图中, 共有9个小长方形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组(即第五组)的频数为
| A.12 | B.24 | C.36 | D.48 |
某医疗研究所为了检验某种血清预防感冒的作用,把 名使用血清的人与另外
名使用血清的人与另外 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设 :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用 列联表计算得
列联表计算得 ,经查对临界值表知
,经查对临界值表知 .
.
对此,四名同学做出了以下的判断: :有
:有 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用” :若某人未使用该血清,那么他在一年中有
:若某人未使用该血清,那么他在一年中有 的可能性得感冒
的可能性得感冒 :这种血清预防感冒的有效率为
:这种血清预防感冒的有效率为
 :这种血清预防感冒的有效率为
:这种血清预防感冒的有效率为
则下列结论中,正确结论的序号是
① ; ②
; ② ;
;
③ ; ④
; ④
| A.①③ | B.②④ | C.①④ | D.都不对 |
设斜率为2的直线 过抛物线
过抛物线 的焦点
的焦点 ,且和
,且和 轴交于点A,若△
轴交于点A,若△ (
( 为坐标原点)的面积为4,则抛物线方程为
为坐标原点)的面积为4,则抛物线方程为
A. |
B. |
C. |
D. |
连结球面上两点的线段称为球的弦.半径为4的球的两条弦 的长度分别等于2
的长度分别等于2 、4
、4 ,
, 分别为
分别为 的中点,每条弦的两端都在球面上运动,有下列四个命题:
的中点,每条弦的两端都在球面上运动,有下列四个命题:
①弦 可能相交于点
可能相交于点 ,②弦
,②弦 可能相交于点
可能相交于点 ,③
,③ 的最大值为5
的最大值为5
④ 的最小值为l.
的最小值为l.
其中真命题的个数为
| A.1个 | B.2个 | C.3个 | D.4个 |
从装有 个球(其中
个球(其中 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出 个球(
个球( ),共有
),共有 种取法,在这
种取法,在这 种取法中,可以分为两类:一类是取出的
种取法中,可以分为两类:一类是取出的 个球全部为白球,另一类是取出的m个球中有1个黑球,共有
个球全部为白球,另一类是取出的m个球中有1个黑球,共有 种取法,即有等式:
种取法,即有等式:
 成立.
成立.
试根据上述思想化简下列式子: _____
_____
(本小题12分)
已知A, B,C为锐角
B,C为锐角 的三个内角,向量
的三个内角,向量
 ,
,
 ,且
,且 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求 取最大值时角
取最大值时角 的大小.
的大小.
(本小题12分)
一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
5 |
 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元. 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求购买该商品的3位顾客中,至少有1位采用1期付款的概率;
(Ⅱ)求 的分布列及期望
的分布列及期望 .
.
(本小题12分)
下图是 一几何体的直观图、主视图、俯视图、左视图.
一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若 为
为 的中点,求证:
的中点,求证:
 面
面 ;
;
(Ⅱ)证明 面
面 ;
;
(Ⅲ)求面 与面
与面 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
(本小题12分)
如图所示,已知圆 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
.
(I)求曲线 的方程;
的方程;
(II)若过定点F(0,2)的直线交曲线 于不同的
于不同的 两点
两点 (点
(点 在点
在点 之间),且满足
之间),且满足 ,求
,求 的取值范围.
的取值范围.
已知函数 ,
, 是
是 的一个零点,又
的一个零点,又 在
在 处有极值,在区间
处有极值,在区间 和
和 上是单调的,且在这两个区间上的单调性相反.
上是单调的,且在这两个区间上的单调性相反.
(I)求 的取值范围;
的取值范围;
(II)当 时,求使
时,求使
 成立的实数
成立的实数 的取值范围.
的取值范围.
(本小题10分)选修4—1:几何证明选讲
如图,设 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径, 是⊙O与l的公共点,
是⊙O与l的公共点,
 ⊥l,
⊥l, ⊥l,垂足分别为
⊥l,垂足分别为 ,
, ,且
,且 ,
,

求证:
(I)l是⊙O的切线;
(II) 平分∠ABD.
平分∠ABD.
(本小题10分)选修4—4:坐标系与参数方程
已知某圆的极坐标方程为
(I)将极坐标方程化为普 通方程,并选择恰当的参数写出它的参数方程;
通方程,并选择恰当的参数写出它的参数方程;
(II)若点 在该圆上,求
在该圆上,求 的最大值和最小值.
的最大值和最小值.
 ,则图中阴影部分表示的集合为
,则图中阴影部分表示的集合为 




 是虚数单位,则设
是虚数单位,则设 是虚数单位,则
是虚数单位,则




 ,则输出的是
,则输出的是








 <1,函数
<1,函数 ,则使
,则使 的x的取值范围是
的x的取值范围是



 ,其中
,其中 ,则导数
,则导数 的取值范围是
的取值范围是



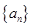 满足
满足 ,它的前
,它的前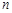 项和为
项和为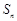 ,则
,则 >1025
>1025 ,则使
,则使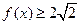 的
的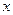 取值范围是______
取值范围是______ 相交于A,B两点,且
相交于A,B两点,且
 =" "
=" " =1(b∈N)的两个焦点
=1(b∈N)的两个焦点 、
、 ,
, 为双曲线上一点,
为双曲线上一点, 成等比数列,则
成等比数列,则 =_____
=_____ ,试比较
,试比较 的大小
的大小 粤公网安备 44130202000953号
粤公网安备 44130202000953号