河南省焦作市高三期末调研数学理卷
已知直线a,b与平面α,给出下列四个命题:
①若a∥b,b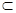 α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b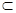 α,则a∥b;
α,则a∥b;
③若a∥α,b∥α,则a∥b; ④若a⊥α,b∥α,则a⊥b.
其中正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
已知函数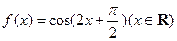 ,下面结论错误的是
,下面结论错误的是
A.函数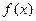 的最小正周期为 的最小正周期为 |
B.函数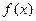 是奇函数 是奇函数 |
C.函数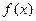 的图象关于直线 的图象关于直线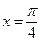 对称 对称 |
D.函数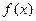 在区间 在区间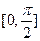 上是减函数 上是减函数 |
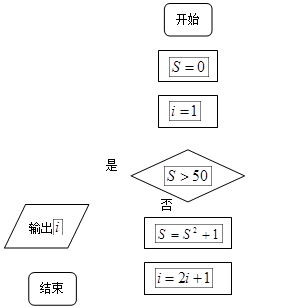
给出定义:若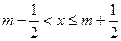 (其中m为整数),则m 叫做离实数x最近的整数,记作
(其中m为整数),则m 叫做离实数x最近的整数,记作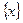 =" m." 在此基础上给出下列关于函数
=" m." 在此基础上给出下列关于函数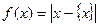 的四个命题:
的四个命题:
①函数y=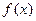 的定义域为R,值域为
的定义域为R,值域为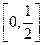 ;
;
②函数y=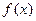 的图像关于直线
的图像关于直线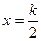 (
(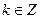 )对称;
)对称;
③函数y=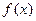 是周期函数,最小正周期为1;
是周期函数,最小正周期为1;
④函数y=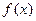 在
在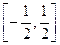 上是增函数.
上是增函数.
其中正确的命题的序号是
| A.① | B.②③ | C.①②③ | D.①④ |
随机地向区域内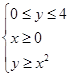 内投点,点落在区域的每个位置是等可能的,则坐标原点与该点连线的倾斜角小于
内投点,点落在区域的每个位置是等可能的,则坐标原点与该点连线的倾斜角小于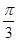 的概率为_________________.
的概率为_________________.
(本小题满分12分)
已知等比数列 中,
中,

 .
.
(Ⅰ)若 为等差数列,且满足
为等差数列,且满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点, PD⊥平面ABCD,且PD=AD= ,CD=1.
,CD=1.
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)证明:MC⊥BD;
(Ⅲ)求二面角A—PB—D的余弦值.
(本小题满分12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率;
(Ⅱ)签约人数 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知椭圆的中心在坐标原点 ,焦点在
,焦点在 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为 一个正方形的顶点.过右焦点
一个正方形的顶点.过右焦点 与
与 轴不垂直的直线
轴不垂直的直线 交椭圆于
交椭圆于 ,
, 两点.
两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在线段 上是否存在点
上是否存在点 ,使得以
,使得以 为邻边的平行四边形是菱形? 若存在,求出
为邻边的平行四边形是菱形? 若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)
已知函数 在
在 上是增函数,
上是增函数, 在
在 上是减函数.
上是减函数.
(Ⅰ)当 的值;
的值;
(Ⅱ)若 在
在 上是增函数,且对于
上是增函数,且对于 内的任意两个变量
内的任意两个变量 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)设 ,求证:
,求证: .
.
请考生在第22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
(Ⅰ)求证:AD∥EC; (Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.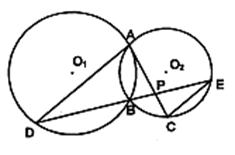
 ,则
,则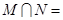
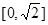
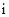 是虚数单位,则
是虚数单位,则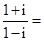
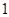
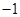
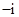
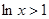 ”是“
”是“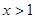 ”的
”的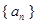 的前
的前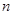 项和为
项和为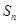 ,且
,且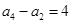 ,
,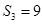 ,则数列
,则数列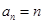
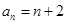
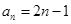
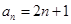
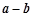 等于
等于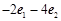
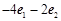
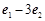
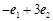
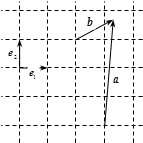
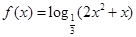 ,则
,则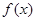 的单调增区间为
的单调增区间为
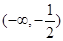
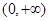
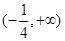
 ,且
,且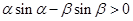 ,则下面结论正确的是
,则下面结论正确的是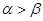
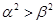
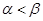
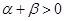
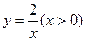 上,且与直线
上,且与直线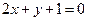 相切的面积最小的圆的方程为
相切的面积最小的圆的方程为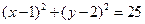
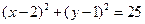
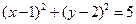
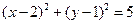
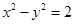 的焦点坐标是____________
的焦点坐标是____________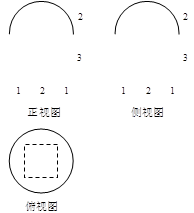
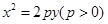 的焦点
的焦点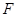 作倾斜角为
作倾斜角为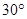 的直线,与抛物线分别交于
的直线,与抛物线分别交于 两点(点
两点(点 在
在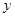 轴的左侧),则
轴的左侧),则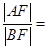 _______________.
_______________.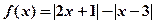 .
.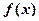 ≤4;(Ⅱ)若存在x使得
≤4;(Ⅱ)若存在x使得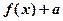 ≤0成立,求实数a的取值范围.
≤0成立,求实数a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号