福建省四地六校联考高二第三次月考理科数学卷
程序框图符号“ ”可用于 ( )
”可用于 ( )
| A.输出a="10" | B.赋值a="10" | C.判断a="10" | D.输入a=10 |
对于任意空间向量 =(a1,a2,a3),
=(a1,a2,a3), =(b1,b2,b3),给出下列三个命题:
=(b1,b2,b3),给出下列三个命题: ①
① ∥
∥
 =
= =
= ②若a1=a2=a3=1,则
②若a1=a2=a3=1,则 为单位向量
为单位向量 ③
③ ⊥
⊥ a1b1+a2b2+a3b3="0 " 其中真命题的个数为( )
a1b1+a2b2+a3b3="0 " 其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
阅读下列程序:
INPUT “n=” ;n
i = 1
f = 1
WHILE
f = f﹡i
i = i+1
WEND
PRINT f
END
如果程序运行后输出720,那么在程序中WHILE后面的条件是 ( )
| A.i >=" 5" | B.i<="5" | C.i >=" 6" | D.i<=6 |
已知曲线 :
: ,则“
,则“ ”是“曲线C表示焦点在
”是“曲线C表示焦点在 轴上的椭圆”的什么条件( )
轴上的椭圆”的什么条件( )
| A.必要不充分 | B.充分不必要 | C.充要 | D.既不充分又不必要 |
下列条件中,使点M与点A、B、C一定共面的为( )
A、 =2
=2 -
- -
- B、
B、 =
= +
+ +
+
C、 +
+ +
+ =
= D、
D、 +
+ +
+ +
+ =
=
打开“几何画板”软件进行如下操作:
①用画图工具在工作区画一个大小适中的图C;
②用取点工具分别在圆C上和圆C外各取一个点A,B;
③用构造菜单下对应命令作出线段AB的垂直平分线 ;
;
④作出直线AC。
设直线AC与直线 相交于点P,当点B为定点,点A在圆C上运动时,点P的轨迹是( )
相交于点P,当点B为定点,点A在圆C上运动时,点P的轨迹是( )
A、椭圆  B、双曲线 C、抛物线 D、圆
B、双曲线 C、抛物线 D、圆
空间四边形OABC,
 =
= ,
, =
= ,
, =
= ,点M在OA上,且OM=2MA,N是BC的中点,则
,点M在OA上,且OM=2MA,N是BC的中点,则 =( )
=( )
A. - - + + |
B.- + + + + |
C. + + - - |
D. + + - - |
已知点P为抛物线 上的动点,点P在y轴上的射影是M,A点坐标为
上的动点,点P在y轴上的射影是M,A点坐标为 ,则
,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D.5 |
已知椭圆 :
: 的焦点分别为
的焦点分别为 ,如果椭圆上存在点
,如果椭圆上存在点 ,使得
,使得 ·
· ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )
A.( ] ] |
B. [ ) ) |
C. ( ] ] |
D.[ ) ) |
如图所示,直线AB的方程为 ,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,
,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,
则飞镖落在阴影部分(三角形ABC的内部)的概率是 ( )
A. |
B. |
C. |
D. |
在60°的二面角的棱上有A,B两点,线段AC,BD分别在二面角的两个面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长度为 .
(本小题满分12分)
给定两个命题, 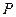 :对任意实数
:对任意实数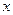 都有
都有 恒成立;
恒成立;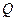 :关于
:关于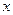 的方程
的方程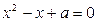 有实数根.如果
有实数根.如果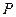 ∨
∨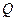 为真命题,
为真命题,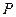 ∧
∧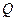 为假命题,求实数
为假命题,求实数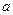 的取值范围.
的取值范围.
(12分) 已知在正方体ABCD —A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG =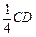 .
. 
(1)求证:EF⊥B1C;
(2)求EF与G C1所成角的余弦值;
(本小题满分12分)在平面直角坐标系xoy中,已知抛物线C: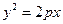 x上横坐标为4的点到该抛物线的焦点的距离为5。
x上横坐标为4的点到该抛物线的焦点的距离为5。
(1)求抛物线C的标准方程;
(2)过点M(1,0)作直线 交抛物线C于A、B两点,求证:
交抛物线C于A、B两点,求证: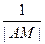 +
+ 恒为定值。
恒为定值。
(本小题满分12分)
某市4997名学生参加高中数学会考,得分均在60分以上,现从中随机抽取一个容量为500的样本,制成如图a所示的频率分布直方图
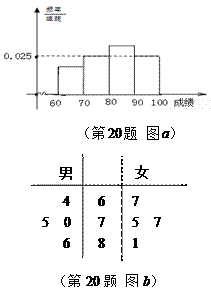
(1)由频率分布直方图可知本次会考的数学平均分为81分.请估计该市得分在区间[60,70]的人数;
(2)如图b所示茎叶图是某班男女各4名学生的得分情况,现用简单随机抽样的方法,从这8名 学生中,抽取男女生各一人,求女生得分不低于男生得分的概率.
学生中,抽取男女生各一人,求女生得分不低于男生得分的概率.
本小题满分12分)
如图,在六面体 中,四边形ABCD是边长为2的正方形,四边形
中,四边形ABCD是边长为2的正方形,四边形 是边长为1的正方形,
是边长为1的正方形, 平面
平面 ,
, 平面ABCD,DD1=2。
平面ABCD,DD1=2。
(1)求证: 与AC共面,
与AC共面, 与BD共面.
与BD共面.
(2)求证:平面
(3)求二面角 的大小.
的大小.
 的焦点坐标为 ( )
的焦点坐标为 ( )



 ,如果
,如果 ,使
,使 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( ) )
) )
) 与双曲线
与双曲线 共渐近线,且过点
共渐近线,且过点 ,则双曲线
,则双曲线 不大于4的概率为 .
不大于4的概率为 . 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 是线段
是线段 上的一点,
上的一点, ,且点
,且点 上.
上. 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程.
上,求椭圆的方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号