2011年初中毕业升学考试(广西桂林卷)数学
用四舍五入法按要求对0.05049分别取近似值,其中错误的是( )
| A.0.1(精确到0.1) | B.0.05(精确到百分位) |
| C.0.05(精确到千分位) | D.0.050(精确到0.001) |
经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为( )
A.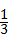 |
B.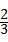 |
C.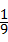 |
D.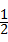 |
如果等腰三角形两边长是6cm和3cm,那么它的周长是( )
| A.9cm | B.12cm |
| C.15cm或12cm | D.15cm |
已知一元二次方程x2+bx﹣3=0的一根为﹣3,在二次函数y=x2+bx﹣3的图象上有三点 、
、 、
、 ,y1、y2、y3的大小关系是( )
,y1、y2、y3的大小关系是( )
| A.y1<y2<y3 | B.y2<y1<y3 |
| C.y3<y1<y2 | D.y1<y3<y2 |
如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为( )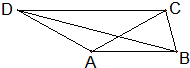
A.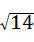 |
B.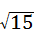 |
C.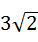 |
D. |
下列判断正确的有( )
①顺次连接对角线互相垂直且相等的四边形的各边中点一定构成正方形;
②中心投影的投影线彼此平行;
③在周长为定值π的扇形中,当半径为 时扇形的面积最大;
时扇形的面积最大;
④相等的角是对顶角的逆命题是真命题.
| A.4个 | B.3个 |
| C.2个 | D.1个 |
如图所示,在梯形ABCD中,AD∥BC,CE是∠BCD的平分线,且CE⊥AB,E为垂足,BE=2AE,若四边形AECD的面积为1,则梯形ABCD的面积为( )
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=30m,BC=70m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
如图所示,四边形ABCD是正方形,点E是边BC 的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
(1)求证:EG=CF;
(2)将△ECF绕点E逆时针旋转90°,请在图中直接画出旋转后的图形,并指出旋转后CF与EG的位置关系.
在同一 直角坐标系中反比例函数
直角坐标系中反比例函数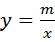 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(﹣2,3),若一次函数的图象又与x轴相交于点
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(﹣2,3),若一次函数的图象又与x轴相交于点 B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.
(1)找出这天载客量的中位数,说明这个中位数的意义;
(2)估计3路公共汽车平均每班的载客量大约是多少?
(3)计算这天载客量在平均载客量以上班次占总班次的百分数.
(注:一个小组的组中值是指这个小组的两个端点数的平均数)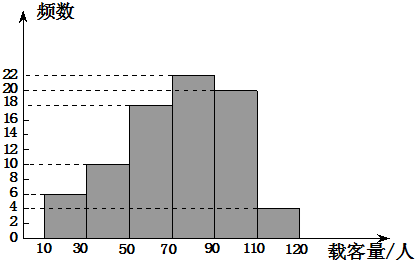
生活中,在分析研究比赛成绩时经常要考虑不等关系.例如:一射击运动员在一次比赛中将进行10次射击,已知前7次射击共中61环,如果他要打破88环(每次射击以1到10的整数环计数)的记录,问第8次射击不能少于多少环?
我们可以按以下思路分析:
首先根据最后二次射击的总成绩可能出现的情况,来确定要打破88环的记录,第8次射击需要得到的成绩,并完成下表:
最后二次射击总成 绩 绩 |
第8次射击需得成绩 |
| 20环 |
|
| 19环 |
|
| 18环 |
|
根据以上分析可得如下解答:
解:设第8次射击的成绩为x环,则可列出一个关于x的不等式:( )解得( )
所以第8次设计不能少于 ( )环
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D, .
.
(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的值.
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成y2=a(x﹣h)2+k的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并在所给的平面直角坐标系中直接画出简图,同时写出该函数在﹣3<x≤ 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;
(3)设一次函数y3=nx+3(n≠0 ),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.
),问是否存在正整数n使得(2)中函数的函数值y=y3时,对应的x的值为﹣1<x<0,若存在,求出n的值;若不存在,说明理由.
如图,已知Rt△ABC中,∠C= 90°,BC="3," AC=4,
90°,BC="3," AC=4,
则sinA的值为( ).
A. |
B. |
C. |
D. |
下面调查中,适合采用全面调查的事件是( ).
| A.对全国中学生心理健康现状的调查. |
| B.对我市食品合格情况的调查. |
| C.对桂林电视台《桂林板路》收视率的调查. |
| D.对你所在的班级同学的身高情况的调查. |
在平面直角坐标系中,将抛物线 绕着它与
绕着它与 轴的交点旋转180°,
轴的交点旋转180°,
所得抛物线的解析式是( ).
A. |
B. |
C. |
D. |
如图,将边长为 的正六边形A1 A2 A3 A4 A5 A6在直线
的正六边形A1 A2 A3 A4 A5 A6在直线 上由图1的位置按顺时针
上由图1的位置按顺时针
方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的
长为( ).
A. |
B. |
C. |
D. |
我市在临桂新区正在建设的广西桂林图书馆、桂林博物馆、桂林大剧院及文化广场,建成后总面积达163500平方米,将成为我市“文化立市”和文化产业大发展的新标志,把163500平方米用科学记数法可表示为 平方米.
如图,等腰梯形ABCD中,AB∥DC,BE∥AD, 梯形ABCD
的周长为26,DE=4,则△BEC的周长为 .
 |
本题满分8分)“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
(1)这次抽查的家长总人数为 ;
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率
是 .
 |
某 市为争创全国文明卫生城,2008年市政府对市区绿化工程投
市为争创全国文明卫生城,2008年市政府对市区绿化工程投
入的资金是2000万元,2010年投入的资金是2420万元,且从2008年到2010年,两年间
每年投入资金的年平均增长率相同.
(1)求该市对市区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该市在2012年需投入多少万元?
某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院
慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一
个老人不足5盒,但至少分得一盒.
(1)设敬老院有 名老人,则这批牛奶共有多少盒?(用含
名老人,则这批牛奶共有多少盒?(用含 的代数式表示).
的代数式表示).
(2)该敬老院至少有多少名老人?最多有多少名老人?
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心, AC长为半径作
AC长为半径作 ⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
(1)求证:D是 弧AE 的中点;
(2)求证:∠DAO =∠B+∠BAD;
(3)若  ,且AC=4,求CF的长.
,且AC=4,求CF的长.
 |



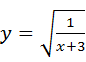 中,自变量x的取值范围( )
中,自变量x的取值范围( ) 可化简为( )
可化简为( ) 的值为( )
的值为( )

 .
. 的倒数是( )
的倒数是( )
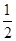
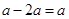
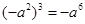

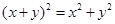
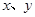 为实数,且
为实数,且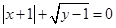 ,则
,则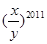 的值是( )
的值是( )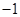

 的倒数是( ).
的倒数是( ).


 、
、 、
、 、
、 中,最小的实数是( ).
中,最小的实数是( ).






 一定经过点( ).
一定经过点( ). ,
, .
. 时,代数式
时,代数式 的值是 .
的值是 . 、
、 在第一象限的图像如图,
在第一象限的图像如图,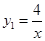 ,过
,过 ,作
,作 轴
轴 ,交
,交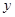 轴于
轴于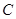 ,若
,若 ,则
,则
 ,
, ,
, ,… ;则
,… ;则 的值为 .(用
的值为 .(用 的代数式表示)
的代数式表示)


 的图象如图.
的图象如图. 轴交点D的坐标;
轴交点D的坐标; 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号