[广东]2014届广东省广州市海珠区高三入学摸底考试文科数学试卷
对于平面 、
、 、
、 和直线
和直线 、
、 、
、 、
、 ,下列命题中真命题是 ( )
,下列命题中真命题是 ( )
A.若 ,则 ,则 ; ; |
B.若 则 则 ; ; |
C.若 ,则 ,则 ; ; |
D.若 ,则 ,则 . . |
给出下列四个结论:
①若命题 ,则
,则 ;
;
② “ ”是“
”是“ ”的充分而不必要条件;
”的充分而不必要条件;
③命题“若 ,则方程
,则方程 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程 没有实数根,则
没有实数根,则 0”;
0”;
④若 ,则
,则 的最小值为
的最小值为 .
.
其中正确结论的个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
已知函数 是定义在
是定义在 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 的值为 ( )
的值为 ( )
| A.-1 | B.-2 | C.2 | D.1 |
已知双曲线 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于 两点,
两点, 为坐标原点.若双曲线的离心率为2,
为坐标原点.若双曲线的离心率为2, 的面积为
的面积为 ,则
,则 .
.
已知极坐标的极点与平面直角坐标系的原点重合,极轴与 轴的正半轴重合,且长度单位相同.圆
轴的正半轴重合,且长度单位相同.圆 的参数方程为
的参数方程为 为参数),点
为参数),点 的极坐标为(
的极坐标为( ,
, ).若点
).若点 是圆
是圆 上的任意一点,
上的任意一点, 两点间距离的最小值为 .
两点间距离的最小值为 .
如图, 是⊙
是⊙ 的直径,
的直径, 是
是 延长线上的一点,过点
延长线上的一点,过点 作⊙
作⊙ 的切线,切点为
的切线,切点为 ,
, ,若
,若 ,则⊙
,则⊙ 的直径
的直径 __________ .
__________ .
某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的的概率.
如图,在四棱锥 中,底面
中,底面 为菱形,其中
为菱形,其中 ,
, ,
, 为
为 的中点.
的中点.
(1) 求证: ;
;
(2) 若平面 平面
平面 ,且
,且 为
为 的中点,求四棱锥
的中点,求四棱锥 的体积.
的体积.
若数列 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 都有
都有 ,记
,记 .
.
(1)求 ,
, 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)若 求证:对任意
求证:对任意 .
.
已知椭圆 :
: 的长轴长为4,且过点
的长轴长为4,且过点 .
.
(1)求椭圆 的方程;
的方程;
(2)设 、
、 、
、 是椭圆上的三点,若
是椭圆上的三点,若 ,点
,点 为线段
为线段 的中点,
的中点, 、
、 两点的坐标分别为
两点的坐标分别为 、
、 ,求证:
,求证: .
.
 满足
满足 (
( 为虚数单位),则
为虚数单位),则 为 ( )
为 ( )



 均为全集
均为全集 的子集,且
的子集,且
 ,
, ,则
,则 ( )
( )


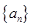 满足
满足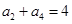 ,
, 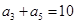 ,则它的前10项和
,则它的前10项和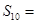 ( )
( ) ,则这四个数的大小关系是 ( )
,则这四个数的大小关系是 ( )



 ,
, ,
, ,若(
,若(
 )
)
 ,则
,则 ( )
( ) 的图像向右平移
的图像向右平移 个单位,那么所得的图像所对应的函数解析式是( )
个单位,那么所得的图像所对应的函数解析式是( )



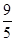 ,则 ( )
,则 ( )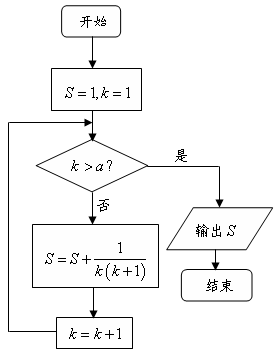
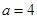


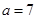
 上随机取一个数
上随机取一个数 ,使得函数
,使得函数 有意义的概率为 .
有意义的概率为 . 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为 .
的最大值为 . 中,角
中,角 的对边分别为
的对边分别为 向量
向量 ,
, ,且
,且 .
. 的值;
的值; ,
, ,求角
,求角 的大小及向量
的大小及向量 在
在 方向上的投影.
方向上的投影. .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号