[浙江]2013届浙江省五校高三下学期第二次联考文科数学试卷
已知等比数列 的公比为
的公比为 ,则“
,则“ ”是“
”是“ 为递减数列”的( )
为递减数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
关于直线 ,
, 及平面
及平面 ,下列命题中正确的是( )
,下列命题中正确的是( )
A.若l∥ ,则l∥m ,则l∥m |
B.若 ∥ ∥ ,m∥ ,m∥ ,则 ,则 ∥m ∥m |
C.若l⊥ ,l∥ ,l∥ ,则 ,则 |
D.若l∥ ,m⊥l,则m⊥ ,m⊥l,则m⊥ |
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
设 ,则函数
,则函数 ( )
( )
A.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
已知 是双曲线
是双曲线 的两个顶点,点
的两个顶点,点 是双曲线上异于
是双曲线上异于 的一点,连接
的一点,连接 (
( 为坐标原点)交椭圆
为坐标原点)交椭圆 于点
于点 ,如果设直线
,如果设直线 的斜率分别为
的斜率分别为 ,且
,且 ,假设
,假设 ,则
,则 的值为( )
的值为( )
| A.1 | B. |
C.2 | D.4 |
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
如图是某几何体的三视图,其中正视图和侧视图是全等的矩形,底边长为2,高为3,俯视图是半径为1的圆,则该几何体的体积是_______.
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图),则这100名同学中学习时间在6~8小时内的人数为 .
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
一个口袋中装有2个白球和3个红球,每次从袋中摸出两个球,若摸出的两个球颜色相同为中奖,否则为不中奖,则中奖的概率为_________.
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
设 为实数,
为实数, 为不超过实数
为不超过实数 的最大整数,记
的最大整数,记 ,则
,则 的取值范围为
的取值范围为 ,现定义无穷数列
,现定义无穷数列 如下:
如下: ,当
,当 时,
时, ;当
;当 时,
时, .如果
.如果 ,则
,则 .
.
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
已知函数 .
.
(Ⅰ)若方程 在
在 上有解,求
上有解,求 的取值范围;
的取值范围;
(Ⅱ)在 中,
中, 分别是A,B,C所对的边,若
分别是A,B,C所对的边,若 ,且
,且 ,
, ,求
,求 的最小值.
的最小值.
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
已知正项数列 的首项
的首项 ,前
,前 项和
项和 满足
满足 .
.
(Ⅰ)求证: 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G、F分别是线段CE、PB的中点.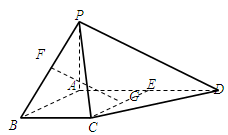
(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求二面角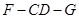 的正切值.
的正切值.
来源:2013届浙江省五校高三下学期第二次联考文科数学试卷
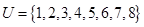 ,集合
,集合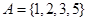 ,
,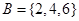 ,则图中的阴影部分表示的集合为( )
,则图中的阴影部分表示的集合为( )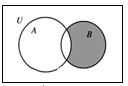
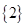
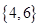
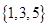
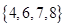
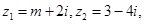 若
若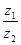 为实数,则实数
为实数,则实数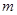 的值为( )
的值为( )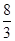
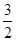
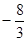
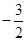
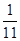 ,则判断框中所填的条件是( )
,则判断框中所填的条件是( )
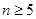
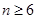
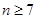

 ,则
,则 =( )
=( ) 满足约束条件
满足约束条件 ,且目标函数
,且目标函数 的最大值等于 ( )
的最大值等于 ( ) 的所有零点之和等于( )
的所有零点之和等于( )
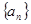 的前
的前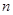 项和为
项和为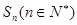 ,若
,若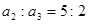 ,则
,则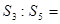 _________.
_________.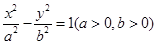 的渐近线与圆
的渐近线与圆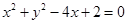 相切,则该双曲线的离心率为_________.
相切,则该双曲线的离心率为_________.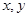 满足
满足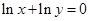 ,且
,且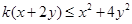 恒成立,则
恒成立,则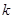 的取值范围是________.
的取值范围是________. .
. 的单调区间;
的单调区间; ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求
成立,求 的范围.
的范围. 的焦点为
的焦点为 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
. 是抛物线上的两点,
是抛物线上的两点, 的角平分线与
的角平分线与 轴垂直,求
轴垂直,求 的面积最大时直线
的面积最大时直线 的方程.
的方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号