四川省成都市高中毕业班摸底测试(文科)数学卷
某学校共有教师200名,其中老年教师25名,中年教师75名,青年教师100名,若采用分层是抽样的方法从这200名教师中抽取40名教师进行座谈,则在青年教师中英抽取的人数为  ( )
( )
| A.15人 | B.20人 | C.25人 | D.30人 |
不等式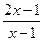 <0的解集是 ( )
<0的解集是 ( )
A.{x|x>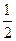 } } |
B.{x|x<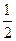 = = |
C.{x|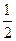 <x<1= <x<1= |
D.{x|x>1或 x< x<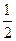 = = |
已知命题p:若x=y,则 ,那么下列叙述正确的是 ( )
,那么下列叙述正确的是 ( )
| A.命题p正确,其逆命题也正确 | B.命题p正确,其逆命题不正确 |
| C.命题p不正确,其逆命题正确 | D.命题p不正确,其逆命题也不正确 |
安排6名演员的演 出顺序时,要求演员甲不第一个出场,也不最后一个出场,则不同的安排方法种数是 ( )
出顺序时,要求演员甲不第一个出场,也不最后一个出场,则不同的安排方法种数是 ( )
| A.120 | B.240 | C.480 | D.720 |
△ABC中内角A、B、C满足2cosAcosC+cosB=0,则此三角形的形状是 ( )
| A.等腰三角形 | B.钝角三角形 |
| C.直角三角形 | D.锐角三角形 |
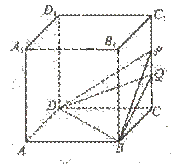
如图,正方体ABCD-A1B1C1D1的棱长为4,点P、Q在
棱CC1上,PQ=1,则三棱锥P-QBD的体积是( )
A.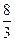 |
B.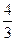 |
| C.8 |
| D.与P点位置有关 |
定义在R上的偶函数f(x-2),当x>-2时,f(x)=ex+1-2(e为自然对数的底数),若存在k∈Z,使
方程f(x)=0的实数根x0∈(k-1 ,k),则k的取值集合是( )
,k),则k的取值集合是( )
| A.{0} | B.(-3) | C.{-4,0} | D.{-3,0} |
在半径为2,球心为O的球面上有两点A、B,若∠AOB= ,则A、B两点间的球面距离为________.
,则A、B两点间的球面距离为________.
经过椭圆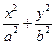 =1(a>b>0)的一个焦点和短轴端点的直线与原点的距离为
=1(a>b>0)的一个焦点和短轴端点的直线与原点的距离为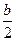 ,则该椭圆的离心率为
,则该椭圆的离心率为
__________________.
已知圆C:x2+y2+2x+Ey+F=0(E、F∈R),有以下命题:①E=-4,F=4是曲线C表示圆的充分非必要条件;②若曲线C与x轴交于两个不同点A(x1,0),B(x2,0),且x1、x2∈[-2,1),则0≤F≤1;③若曲线C与x轴交于两个不同点A(x1,0),B(x2,0),且x1、x2∈[-2,1),O为坐标原点 ,则|
,则| |的最大值为2;④若E=2F,则曲线C表示圆,且该圆面积的最大值为
|的最大值为2;④若E=2F,则曲线C表示圆,且该圆面积的最大值为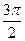 . 其中所有正确命题的序号是____________.
. 其中所有正确命题的序号是____________.
(本小题满分12分)某 公司购买了一博览会门票10张,其中甲类票4张,乙类票6张,现从这10张票中任取3张奖励一名员工.
公司购买了一博览会门票10张,其中甲类票4张,乙类票6张,现从这10张票中任取3张奖励一名员工.
(1)求该员工得到甲类票2张,乙类票1张的概率;
(2)求该员工得到甲类票1张数的概率,
(本小题满分12分)已知向量 =(sin2x,cos2x),
=(sin2x,cos2x), =(cos
=(cos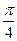 ,sin
,sin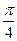 ),函数f(x)=
),函数f(x)= +2a(其中a为实常数)
+2a(其中a为实常数)
(1)求函数f(x)的最小正周期;
(2)若x∈[0,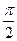 ]时,函数f(x)的最小值为-2,求a的值.
]时,函数f(x)的最小值为-2,求a的值.
(本小题满分12分)如图,在四边形ABCD中,AC⊥BD,垂足为O,PO⊥平面ABCD,AO=BO=DO=1,CO=PO=2,E是线段PA上的点,AE∶AP=1∶3.
(1) 求证:OE∥平面PBC;
(2)求二面角D-P B-C的大小.
B-C的大小.
(本小题满分 12分)已知等差数列{an2
12分)已知等差数列{an2 }中,首项a12=1,公差d=1,an>0,n∈N
}中,首项a12=1,公差d=1,an>0,n∈N *.
*.
(1)求数列{an}的通项公式;
(2)设bn= ,数列{bn}的前120项和T120;
,数列{bn}的前120项和T120;
(本小题满分12分)设直线l(斜率存在)交抛物线y2=2px(p>0,且p是常数)于两个 不同点A(x1,y1),B(x2,y2),O为坐标原点,且满足
不同点A(x1,y1),B(x2,y2),O为坐标原点,且满足 =x1x2+2(y1+y2).
=x1x2+2(y1+y2).
(1)求证:直线l过定点;
(2)设(1)中的定点为P,若点M在射线PA上,满足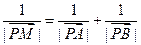 ,求点M
,求点M
的轨迹方程.
 ( )
( )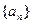 中,若
中,若 则
则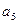 的值是
的值是 

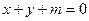 与圆
与圆 相切,则实数m的值为
相切,则实数m的值为


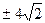
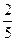 ,则sin2α= ( )
,则sin2α= ( )

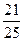
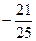
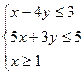 ,则2x+y的最大值为 ( )
,则2x+y的最大值为 ( ) 是________________
是________________
 数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk, )当Φ(x)=2x时 ①求f0(x)和fk
)当Φ(x)=2x时 ①求f0(x)和fk (x)
(x) 的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线; 粤公网安备 44130202000953号
粤公网安备 44130202000953号